题目内容
14.对函数f(x)=ax2+bx+c(a≠0)作x=h(t)的代换,则一定不改变函数f(x)值域的代换是( )| A. | h(t)=10t | B. | h(t)=log2t | C. | h(t)=t2 | D. | $h(t)=\frac{1}{t}$ |
分析 求出二次函数的定义域和值域,对选项分析,求出它们的值域,与R比较,即可判断B正确,A,C,D不正确.
解答 解:函数f(x)=ax2+bx+c(a≠0)的定义域为R,
a>0时,函数的值域为[$\frac{4ac-{b}^{2}}{4a}$,+∞);
a<0时,函数的值域为(-∞,$\frac{4ac-{b}^{2}}{4a}$].
对于A,h(t)=10t>0,可能改变f(x)的值域;
对于B,h(t)=log2t的值域为R,与f(x)的定义域相同,不改变f(x)的值域;
对于C,h(t)=t2的值域为[0,+∞),可能改变f(x)的值域;
对于D,h(t)=$\frac{1}{t}$的值域为(-∞,0)∪(0,+∞),可能改变f(x)的值域.
故选:B.
点评 本题考查函数的性质和运用,主要考查二次函数、指数函数和对数函数和幂函数的值域,属于基础题.

练习册系列答案
相关题目
2.已知函数f(x)=x2-kx-1在[5,+∞)上单调递增,则k的取值范围是( )
| A. | (-∞,10) | B. | (-∞,10] | C. | [10,+∞) | D. | (10,+∞) |
6.若cos(π-α)=$\frac{4}{5}$,且α是第二象限角,则sinα的值为( )
| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
4.函数f(x)=$\sqrt{4-x^2}$-log2x的值域为( )
| A. | (-∞,-1) | B. | (-∞,1] | C. | [-1,+∞) | D. | (-1,+∞) |
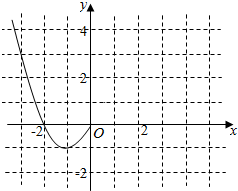 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.