题目内容
3．
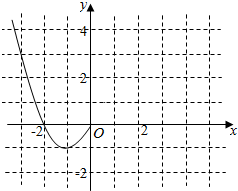
已知函数f（x）是定义在R上的偶函数，且当x≤0时，f（x）=x2+2x．（1）现已画出函数f（x）在y轴左侧的图象，如图所示，请补充画出函数f（x）的完整图象，并根据图象写出函数f（x）的单调区间；
（2）已知关于x的方程f（x）=m有两个不等的实根，求实数m的取值范围．
分析 （1）根据偶函数的图象关于y轴对称，可补充函数图象，数形结合可得函数f（x）的单调区间；
（2）根据函数图象，分析图象与y=m的交点情况，可得关于x的方程f（x）=m有两个不等的实根时，实数m的取值范围．
解答 解：（1）∵偶函数的图象关于y轴对称，
故函数图象如下图所示：
由图可得：
函数的单调递增区间为：（-1，0]，（1，+∞），
函数的单调递减区间为：（-∞，-1]，（0，1]；
（2）方程f（x）=m根的个数，等同于图象与y=m的交点个数，
由图可得方程f（x）=m有两个不等的实根，
即图象与y=m的有两个交点，
则m∈（0，+∞）∪{-1}．
点评 本题考查的知识点是函数奇偶性的性质，熟练掌握函数奇偶性的性质，是解答的关键．
练习册系列答案
相关题目
设函数f（x）=loga（2x+1）在区间$（{-\frac{1}{2}，0}）$上满足f（x）＞0．
14．对函数f（x）=ax2+bx+c（a≠0）作x=h（t）的代换，则一定不改变函数f（x）值域的代换是（ ）
| A． | h（t）=10t | B． | h（t）=log2t | C． | h（t）=t2 | D． | $h（t）=\frac{1}{t}$ |
8．f（x）为定义域R，图象关于原点对称，当x≥0时，f（x）=2x+2x+b（b为常数），则x＜0时，f（x）解析式为（ ）
| A． | f（x）=2x-2x-1 | B． | f（x）=-2-x+2x+1 | C． | f（x）=2-x-2x-1 | D． | f（x）=-2-x-2x+1 |