题目内容
(本小题满分12分)
已知函数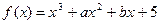 ,在函数
,在函数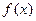 图像上一点
图像上一点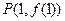 处切线的斜率为3.
处切线的斜率为3.
(1)若函数 在
在 时有极值,求
时有极值,求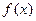 的解析式;
的解析式;
(2 )若函数
)若函数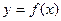 在区间
在区间 上单调递增,求
上单调递增,求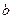 的取值范围.
的取值范围.
已知函数
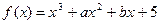 ,在函数
,在函数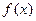 图像上一点
图像上一点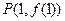 处切线的斜率为3.
处切线的斜率为3.(1)若函数
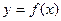 在
在 时有极值,求
时有极值,求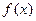 的解析式;
的解析式; (2
 )若函数
)若函数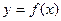 在区间
在区间 上单调递增,求
上单调递增,求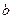 的取值范围.
的取值范围.解:由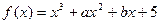
求导数得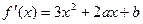 ,
,
由在函数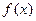 图像上一点
图像上一点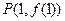 处切线的斜率为3,
处切线的斜率为3,
知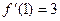 ,即
,即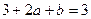 ,
,
化简得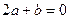 …… ① …………………2分
…… ① …………………2分
(1) 因为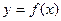 在
在 时有极值,
时有极值,
所以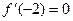 ,
,
即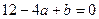 …… ②
…… ②
由①②联立解得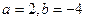 ,
,
∴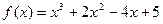 .…………………6分
.…………………6分
(2)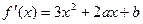 ,
,
由①知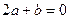 ,
,
∴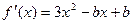 .
.
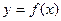 在区间
在区间 上单调递增,
上单调递增,
依题意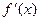 在
在 上恒有
上恒有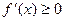 ,………8分
,………8分
即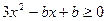 在
在 上恒成立,
上恒成立,
下面讨论函数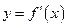 的对称轴:
的对称轴:
① 在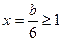 时,
时,
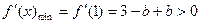 ,
,
∴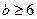 .…………………9分
.…………………9分
② 在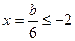 时,
时,
 ,
,
无实数解.…………………10分
③ 在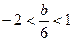 时,
时,
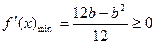 ,
,
∴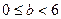 .…………………11分
.…………………11分
综合上述讨论可知,
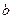 的取值范围是
的取值范围是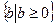 .…………………12分
.…………………12分
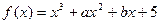
求导数得
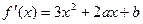 ,
,由在函数
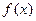 图像上一点
图像上一点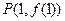 处切线的斜率为3,
处切线的斜率为3,知
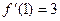 ,即
,即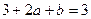 ,
,化简得
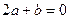 …… ① …………………2分
…… ① …………………2分(1) 因为
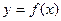 在
在 时有极值,
时有极值,所以
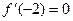 ,
,即
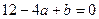 …… ②
…… ②由①②联立解得
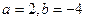 ,
,∴
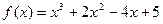 .…………………6分
.…………………6分(2)
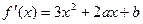 ,
,由①知
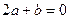 ,
,∴
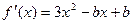 .
.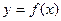 在区间
在区间 上单调递增,
上单调递增,依题意
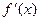 在
在 上恒有
上恒有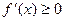 ,………8分
,………8分即
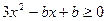 在
在 上恒成立,
上恒成立,下面讨论函数
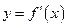 的对称轴:
的对称轴:① 在
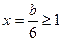 时,
时,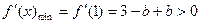 ,
,∴
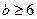 .…………………9分
.…………………9分② 在
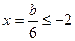 时,
时, ,
,无实数解.…………………10分
③ 在
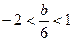 时,
时,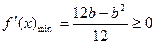 ,
,∴
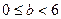 .…………………11分
.…………………11分综合上述讨论可知,
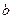 的取值范围是
的取值范围是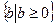 .…………………12分
.…………………12分略

练习册系列答案
相关题目
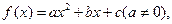 曲线y=f(x)通过点(0,2a+3),且
曲线y=f(x)通过点(0,2a+3),且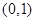 且与曲线
且与曲线 在点
在点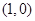 处切线垂直的直线方程是( )
处切线垂直的直线方程是( )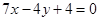
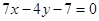
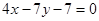

 可导,则
可导,则 等于( )
等于( ) B
B 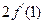 C
C 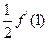 D
D 
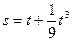 (
(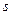 的单位为m), 则当
的单位为m), 则当 时的瞬时速度是
时的瞬时速度是 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为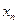 ,则
,则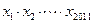 的值为( )
的值为( ) 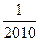
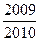
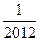
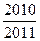
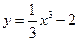 在点(
在点(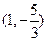 处切线的倾斜角为( )
处切线的倾斜角为( )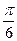
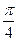
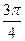
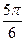

 是
是