题目内容
（本小题满分12分）
设函数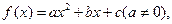
曲线y=f(x)通过点（0，2a+3），且
在点（-1，f（-1））处的切线垂直于y轴.
（Ⅰ）用a分别表示b和c；
（Ⅱ）当bc取得最小值时，求函数g(x)=-f(x)e-x的单调区间.
设函数
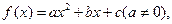曲线y=f(x)通过点（0，2a+3），且在点（-1，f（-1））处的切线垂直于y轴.
（Ⅰ）用a分别表示b和c；
（Ⅱ）当bc取得最小值时，求函数g(x)=-f(x)e-x的单调区间.
解：(Ⅰ)因为
又因为曲线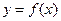
通过点（0，2a+3）,
故
………2分
又曲线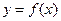在（-1，f(-1)）处的切线垂直于y轴，故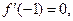
即-2a+b=0,因此b=2a. ………5分
(Ⅱ)由(Ⅰ)得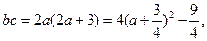
故当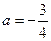
时，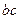
取得最小值-
.
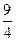此时有
………7分
从而
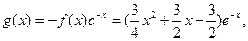
所以
………9分
令
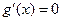，解得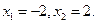
当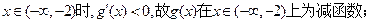
当
当
由此可见，函数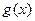
的单调递减区间为（-∞，-2）和（2，+∞）；单调递增区间为（-2，2）…12分
又因为曲线
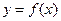通过点（0，2a+3）,故
………2分又曲线
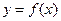在（-1，f(-1)）处的切线垂直于y轴，故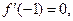即-2a+b=0,因此b=2a. ………5分
(Ⅱ)由(Ⅰ)得
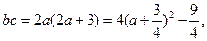
故当
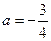时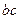，取得最小值-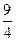.此时有
………7分从而
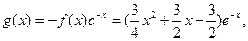
所以
………9分令
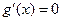，解得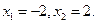当
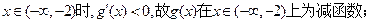
当
当
由此可见，函数
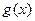的单调递减区间为（-∞，-2）和（2，+∞）；单调递增区间为（-2，2）…12分略
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
，
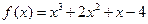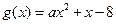，若对任意的
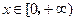都有
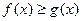，求实数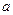
的取值范围．
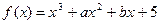，在函数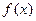
图像上一点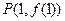
处切线的斜率为3．
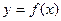在
时有极值，求
）若函数
上单调递增，求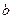
的取值范围．
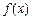为可导函数，
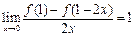，则在点（1，
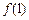）处的切线斜率为
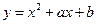在点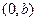
处的切线方程是
，则 ( )
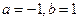
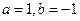
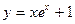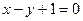
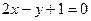
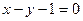
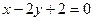
在点（0，1）处的切线方程是 （ ）
2分别表示乌龟和兔子所行的路程，t为时间，则下列图象中与故事情节相吻合的是（ ）