题目内容
18.已知关于实数x的两个命题:p:$\frac{x+1}{2-x}$<0,q:x+a<0,且命题p是q的必要不充分条件,则实数a的取值范围是a≥1.分析 根据不等式的解法求出p,q的等价条件,然后利用充分条件和必要条件的定义即可得到结论.
解答 解:p:$\frac{x+1}{2-x}$<0?(x+1)(x-2)>0,解得x<-1,或x>2,
q:x+a<0,解得x<-a,
∵命题p是q的必要不充分条件,
∴-a≤-1,
即a≥1
故答案为:a≥1.
点评 本题主要考查充分条件和必要条件的应用,利用不等式的性质求出p,q的等价条件是解决本题的关键

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
13.已知M(3,-2),N(-5,-1),若$\overrightarrow{MP}=\frac{1}{2}\overrightarrow{MN}$,则P点的坐标为( )
| A. | (-8,1) | B. | (8,-1) | C. | $(-1,-\frac{3}{2})$ | D. | $(1,\frac{3}{2})$ |
10.等差数列{an},{bn}的前n项和分别为Sn,Tn,若$\frac{{S}_{n}}{{T}_{n}}$=$\frac{2n+4}{3n+1}$,则an=bn时n=( )
| A. | 2 | B. | 6 | C. | 无解 | D. | 无数多个 |
7. 正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )
正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )
 正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )
正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )| A. | 20152 | B. | 20162 | C. | 2015+2016 | D. | 2015×2016 |
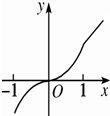
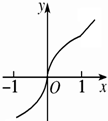
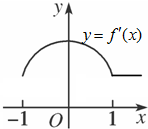 已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象可能是( )
已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象可能是( )