题目内容
已知函数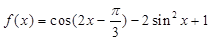 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
:(1)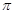 ;(2)
;(2)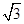 ;
;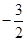 .
.
解析试题分析:(1)先利用和差化积公式以及二倍角公式,将原式化为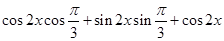 ,再利用积化和差公式将此式变形化简得到:
,再利用积化和差公式将此式变形化简得到: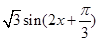 ,再根据公式:
,再根据公式: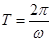 ,求出所给函数的周期;(2)根据已知条件
,求出所给函数的周期;(2)根据已知条件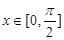 ,求出
,求出 ,再依据函数
,再依据函数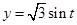 ,在
,在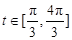 上的单调性得到:函数
上的单调性得到:函数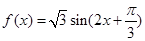 在
在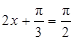 时取得最大值,在
时取得最大值,在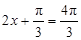 时取得最小值,并分别求出最大值和最小值以及对应的
时取得最小值,并分别求出最大值和最小值以及对应的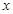 的值.
的值.
试题解析:(1)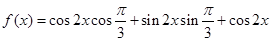

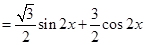
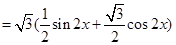
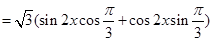
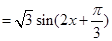 5分
5分
所以 的最小正周期为
的最小正周期为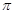 . 7分
. 7分
(2)由(1)知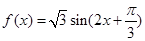 ,
,
因为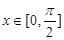 ,所以
,所以 .
.
当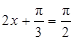 ,即
,即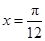 时,函数
时,函数 取最大值
取最大值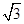 ;
;
当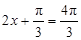 ,即
,即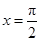 时,函数
时,函数 取最小值
取最小值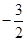 .
.
所以,函数 在区间
在区间 上的最大值为
上的最大值为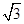 ,最小值为
,最小值为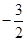 . 13分
. 13分
考点:1.和差化积公式;2.三角函数的周期;3.三角函数的单调性;4.三角函数的最值;5.二倍角公式

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
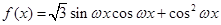 ,
,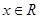 ,
,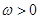 .
.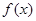 的值域;
的值域; 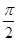 ,则当
,则当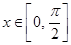 时,求
时,求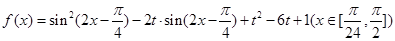 其最小值为
其最小值为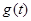 .
.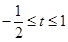 时,要使关于
时,要使关于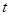 的方程
的方程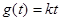 有一个实根,求实数
有一个实根,求实数 的取值范围.
的取值范围. .
. 的最小正周期和值域;
的最小正周期和值域; 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 且
且 ,
, ,求
,求 和
和 .
. ,且
,且 ,求
,求 的值。
的值。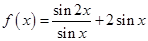 .
.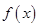 的定义域和最小正周期;
的定义域和最小正周期;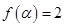 ,
,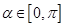 ,求
,求 的值.
的值.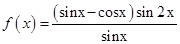 .
.  的定义域及最小正周期;
的定义域及最小正周期;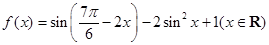 ,
,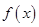 的周期及单调递增区间;
的周期及单调递增区间;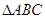 中,三内角
中,三内角 ,
,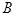 ,
, 的对边分别为
的对边分别为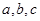 ,已知函数
,已知函数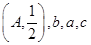 成等差数列,且
成等差数列,且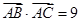 ,求
,求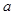 的值.
的值. ,cos(α+β)=-
,cos(α+β)=- ,求cos(α-β)的值.
,求cos(α-β)的值.