题目内容
(本小题满分16分)
已知函数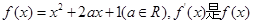 的导函数。
的导函数。
(1)若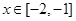 ,不等式
,不等式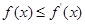 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(2)解关于x的方程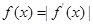 ;
;
(3)设函数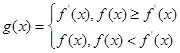 ,求
,求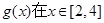 时的最小值;
时的最小值;
已知函数
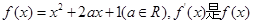 的导函数。
的导函数。(1)若
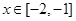 ,不等式
,不等式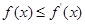 恒成立,求a的取值范围;
恒成立,求a的取值范围;(2)解关于x的方程
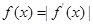 ;
;(3)设函数
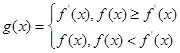 ,求
,求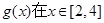 时的最小值;
时的最小值;(1)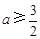 . ⑵
. ⑵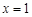 或
或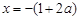 .
.
⑶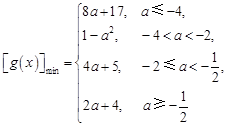
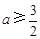 . ⑵
. ⑵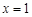 或
或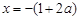 .
.⑶
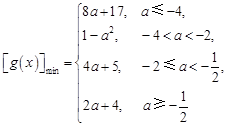
本试题主要是考查了导数在研究函数中的运用,利用导数求解函数单调区间,以及解方程和运用导数求解分段函数的最值的综合运用。
(1)第一问根据已知条件,得到不等式的恒成立问题就是分离参数法,来求解参数的取值范围的转化思想的运用。
(2)第二问解方程关键是将原式整理为关于形如二次方程的形式,然后对于绝对值讨论去掉符号,得到方程的解。
(3)分段函数的最值,就是利用各段函数的单调性求解得到最值,再比较大小得到。
(1)因为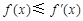 ,所以
,所以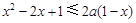 ,
,
又因为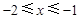 ,
,
所以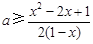 在
在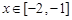 时恒成立,因为
时恒成立,因为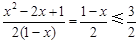 ,
,
所以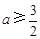 .……………………………………………………………………………4分
.……………………………………………………………………………4分
⑵ 因为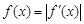 ,所以
,所以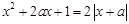 ,
,
所以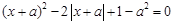 ,则
,则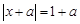 或
或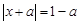 . ……………7分
. ……………7分
①当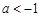 时,
时,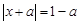 ,所以
,所以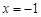 或
或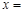
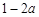 ;
;
②当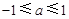 时,
时,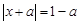 或
或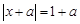 ,
,
所以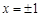 或
或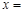
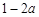 或
或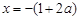 ;
;
③当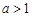 时,
时,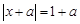 ,所以
,所以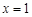 或
或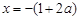 .…………………………10分
.…………………………10分
⑶因为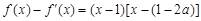 ,
,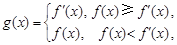
① 若 ,则
,则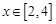 时,
时,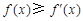 ,所以
,所以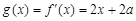 ,
,
从而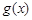 的最小值为
的最小值为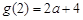 ; ………………………………12分
; ………………………………12分
②若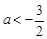 ,则
,则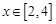 时,
时,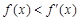 ,所以
,所以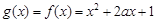 ,
,
当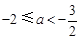 时,
时,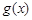 的最小值为
的最小值为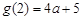 ,
,
当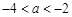 时,
时,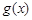 的最小值为
的最小值为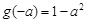 ,
,
当 时,
时,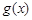 的最小值为
的最小值为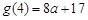 .…………………………………14分
.…………………………………14分
③若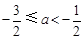 ,则
,则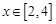 时,
时,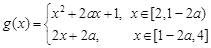
当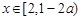 时,
时,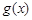 最小值为
最小值为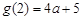 ;
;
当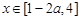 时,
时,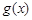 最小值为
最小值为 .
.
因为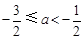 ,
,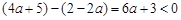 ,
,
所以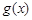 最小值为
最小值为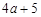 .综上所述,
.综上所述,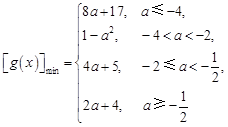 …………………………………………16分
…………………………………………16分
(1)第一问根据已知条件,得到不等式的恒成立问题就是分离参数法,来求解参数的取值范围的转化思想的运用。
(2)第二问解方程关键是将原式整理为关于形如二次方程的形式,然后对于绝对值讨论去掉符号,得到方程的解。
(3)分段函数的最值,就是利用各段函数的单调性求解得到最值,再比较大小得到。
(1)因为
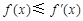 ,所以
,所以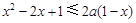 ,
,又因为
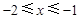 ,
,所以
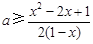 在
在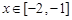 时恒成立,因为
时恒成立,因为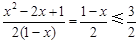 ,
,所以
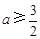 .……………………………………………………………………………4分
.……………………………………………………………………………4分⑵ 因为
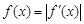 ,所以
,所以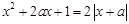 ,
,所以
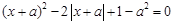 ,则
,则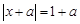 或
或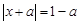 . ……………7分
. ……………7分①当
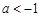 时,
时,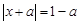 ,所以
,所以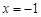 或
或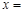
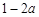 ;
;②当
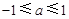 时,
时,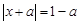 或
或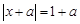 ,
,所以
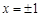 或
或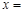
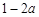 或
或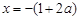 ;
;③当
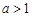 时,
时,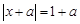 ,所以
,所以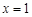 或
或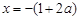 .…………………………10分
.…………………………10分⑶因为
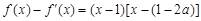 ,
,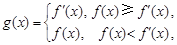
① 若
 ,则
,则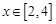 时,
时,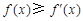 ,所以
,所以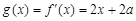 ,
,从而
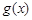 的最小值为
的最小值为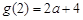 ; ………………………………12分
; ………………………………12分②若
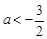 ,则
,则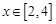 时,
时,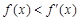 ,所以
,所以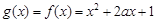 ,
,当
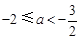 时,
时,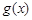 的最小值为
的最小值为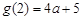 ,
,当
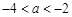 时,
时,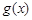 的最小值为
的最小值为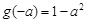 ,
,当
 时,
时,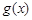 的最小值为
的最小值为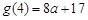 .…………………………………14分
.…………………………………14分③若
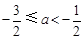 ,则
,则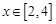 时,
时,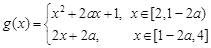
当
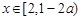 时,
时,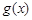 最小值为
最小值为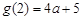 ;
;当
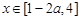 时,
时,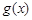 最小值为
最小值为 .
.因为
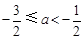 ,
,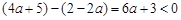 ,
,所以
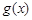 最小值为
最小值为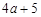 .综上所述,
.综上所述,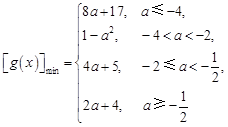 …………………………………………16分
…………………………………………16分
练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
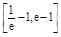 时,不等式f(x)<m恒成立,求实数m的值;
时,不等式f(x)<m恒成立,求实数m的值;
 =
= 时,求曲线
时,求曲线 在点(
在点( ,
, )处的切线方程。
)处的切线方程。 若不存在,说明理由。若存在,求出
若不存在,说明理由。若存在,求出 ,函数
,函数 .
. 时,
时, ,求函数
,求函数 的单调区间;
的单调区间; 的不等式
的不等式 在区间
在区间 上有解,求
上有解,求 的取值范围;
的取值范围; 在其图象上的两点
在其图象上的两点 ,
, (
(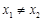 )处的切线分别为
)处的切线分别为 .若直线
.若直线 与
与 平行,试探究点
平行,试探究点 与点
与点 的关系,并证明你的结论.
的关系,并证明你的结论.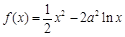 ,
,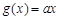
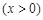 .
.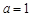 时,求
时,求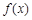 的单调递增区间;
的单调递增区间;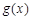 的图象的上方,求实数
的图象的上方,求实数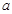 的取值范围.
的取值范围. .
.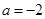 时,求函数
时,求函数 的单调区间;
的单调区间; ,使得函数
,使得函数 ?若存在,,求
?若存在,,求 ,总有
,总有 ,则称
,则称 是
是 的凸
的凸 ,则称
,则称 时,利用定义分析
时,利用定义分析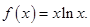
 的极值点;
的极值点;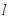 过点
过点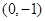 且与曲线
且与曲线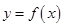 相切,求直线
相切,求直线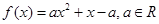 。
。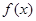 有最大值
有最大值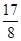 ,求实数
,求实数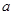 的值;
的值;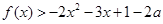 对一切实数
对一切实数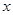 恒成立,求实数
恒成立,求实数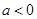 ,解不等式
,解不等式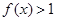 。
。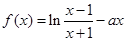 在
在 上单调递增,则实数a的取值范围是 .
上单调递增,则实数a的取值范围是 .