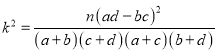题目内容
【题目】已知抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的右焦点相同.
的右焦点相同.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() ,
,![]() 都只有一个公共点,记直线
都只有一个公共点,记直线![]() 与抛物线
与抛物线![]() 的公共点为
的公共点为![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)求出椭圆的焦点坐标,即得抛物线焦点坐标,可得抛物线方程;
(2)说明斜率不存在的直线不可能是公切线,斜率存在时,设方程为![]() ,由两个相切,即相应的
,由两个相切,即相应的![]() ,求得
,求得![]() ,从而得切点坐标.
,从而得切点坐标.
(1)由已知可得椭圆![]() 的
的![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() ,因此椭圆
,因此椭圆![]() 的右焦点为
的右焦点为![]() .
.
于是,由![]() ,得
,得![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 的斜率不存在时,显然不满足题意.
的斜率不存在时,显然不满足题意.
当直线![]() 的斜率不存在时,显然不满足题意.
的斜率不存在时,显然不满足题意.
当直线![]() 的斜率存在时,可设直线
的斜率存在时,可设直线![]() 的方程为
的方程为![]() .
.
联立![]() 与
与![]() ,得方程组,消去
,得方程组,消去![]() ,整理,得
,整理,得![]() ,
,
所以![]() ,即
,即![]() .(*)
.(*)
联立![]() 与
与![]() ,得方程组,消去
,得方程组,消去![]() ,整理,得
,整理,得![]() .
.
∴![]() ,即
,即![]() .(**)
.(**)
由(*)和(**)得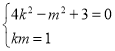 ,所以
,所以![]()
![]() ,
,
其对应的![]() .
.
将![]() 的值代入方程
的值代入方程![]() ,解得
,解得![]() ,进而
,进而![]() .
.
经检验![]() 或
或![]() 符合题意,为所求.
符合题意,为所求.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目