题目内容
3.5名男生、2名女生站一排照相:(1)若女生甲要站两端,有多少种不同的站法?
(2)若两名女生都不站在两端,有多少不同的站法?
(3)若两名女生不相邻,有多少种不同的站法?
(4)若站一排,且女生甲要在女生乙的右方,有多少种不同的站法?
分析 (1)根据题意,分2步进行分析:第一步:让女生甲站排头或排尾,第二步:剩余6人站其它6个位置,进行全排列即可,由分步计数原理计算可得答案;
(2)根据题意,分2步进行分析:第一步:从中间5个位置选2个站两个女生,第二步:剩余5人站其它5个位置,将5人进行全排列即可,由分步计数原理计算可得答案;
(3)根据题意,分2步进行分析:第一步:将5个男生进行排列,第二步:从6个空中选2个给两名女生排列,求出每一步的情况数目,由分步计数原理计算可得答案;
(4)根据题意,首先将7人站成一排进行全排列,由于女生甲在女生乙右方和左方的排法数目相同,由倍分法计算可得答案.
解答 解:(1)根据题意,分2步进行分析:
第一步:让女生甲站排头或排尾,有2种站法;
第二步:剩余6人站其它6个位置,共有$A_6^6$种站法.
由分步计数原理得,女生甲站两端,共有$2×A_6^6=1440$种站法.
(2)根据题意,分2步进行分析:
第一步:从中间5个位置选2个站两个女生,有$A_5^2=20$种站法;
第二步:剩余5人站其它5个位置,有A55=120种站法.
由分步计数原理得,两个女生都不站在两端共有A52A55=2400种站法.
(3)根据题意,分2步进行分析:
第一步:将5个男生进行排列,有A55种站法;
第二步:从6个空中选2个给两名女生排列,有A62种站法.
由分步计数原理得,两个女生不相邻有A55A62=3600种站法.
(4)7人站成一排,有A77种排法,
由于女生甲在女生乙右方和左方的可能性相同,即排法数目相同,
故共有$\frac{{A}_{7}^{7}}{2}$=2520种站法.
点评 本题考查排列、组合的运用,涉及分类、分步计数原理原理的应用,注意常见问题的处理方法.

练习册系列答案
相关题目
13.P为抛物线x2=-4y上一点,A(1,0),则点P到此抛物线的准线的距离与P到点A的距离之和的最小值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{2}$ |
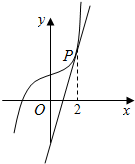 如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.
如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.