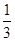题目内容
已知函数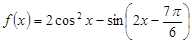 .
.
(1)求函数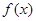 的最大值,并写出
的最大值,并写出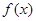 取最大值时
取最大值时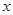 的取值集合;
的取值集合;
(2)已知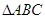 中,角
中,角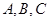 的对边分别为
的对边分别为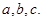 若
若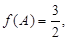
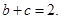 求实数
求实数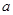 的最小值.
的最小值.
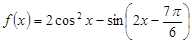 .
.(1)求函数
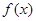 的最大值,并写出
的最大值,并写出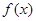 取最大值时
取最大值时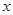 的取值集合;
的取值集合;(2)已知
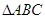 中,角
中,角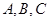 的对边分别为
的对边分别为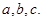 若
若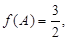
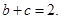 求实数
求实数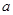 的最小值.
的最小值.(1) ;(2)实数
;(2)实数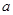 取最小值1
取最小值1
 ;(2)实数
;(2)实数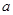 取最小值1
取最小值1试题分析:(1)先用诱导公式化为二倍角,再用两角和的正弦化为一个三角函数,然后求使得

成立时x的集合即可;


(2)利用已知中
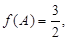 求出A角的值,在△ABC中根据余弦定理用含b,c的代数式表示a的平方,再由
求出A角的值,在△ABC中根据余弦定理用含b,c的代数式表示a的平方,再由b与c的和为定值利用均值不等式从而求出a的最小值.
试题解析:(1)

 .
.∴函数
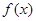 的最大值为
的最大值为 .要使
.要使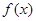 取最大值,则
取最大值,则
 ,解得
,解得 .
.故
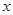 的取值集合为
的取值集合为 . 6分
. 6分(2)由题意,
 ,化简得
,化简得 
 ,
,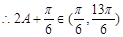 ,∴
,∴ , ∴
, ∴
在
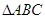 中,根据余弦定理,得
中,根据余弦定理,得 .
.由
 ,知
,知 ,即
,即 .
.∴当
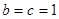 时,实数
时,实数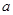 取最小值
取最小值 12分
12分
练习册系列答案
相关题目
 的取值范围是_______ .
的取值范围是_______ .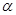 ,
,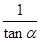 是关于x的方程x2-kx+k2-3=0的两个实根,且3π<
是关于x的方程x2-kx+k2-3=0的两个实根,且3π<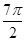 ,则cos
,则cos
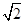
 是
是 边
边 延长线上一点,记
延长线上一点,记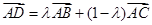 . 若关于
. 若关于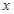 的方程
的方程 在
在 上恰有两解,则实数
上恰有两解,则实数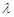 的取值范围是( )
的取值范围是( )
 或
或
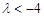 或
或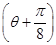 =
=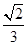 ,求tan θ的值.
,求tan θ的值. 中,
中, ,则
,则 等于 .
等于 . 为集合{a1,a2,…,an}相对a0的“正弦方差”,则集合
为集合{a1,a2,…,an}相对a0的“正弦方差”,则集合 相对a0的“正弦方差”为( )
相对a0的“正弦方差”为( )