题目内容
已知函数f(x)=2sin xcos x+cos 2x(x∈R).
(1)当x取什么值时,函数f(x)取得最大值,并求其最大值;
(2)若θ为锐角,且f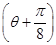 =
=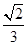 ,求tan θ的值.
,求tan θ的值.
(1)当x取什么值时,函数f(x)取得最大值,并求其最大值;
(2)若θ为锐角,且f
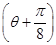 =
=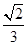 ,求tan θ的值.
,求tan θ的值.(1) x=kπ+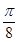 (k∈Z)时,函数f(x)取得最大值,其最大值为
(k∈Z)时,函数f(x)取得最大值,其最大值为 .
.
(2)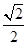
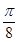 (k∈Z)时,函数f(x)取得最大值,其最大值为
(k∈Z)时,函数f(x)取得最大值,其最大值为 .
.(2)
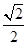
解:(1)f(x)=2sin xcos x+cos 2x
=sin 2x+cos 2x
=
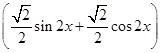
= sin
sin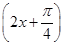 .
.
∴当2x+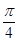 =2kπ+
=2kπ+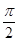 (k∈Z),即x=kπ+
(k∈Z),即x=kπ+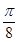 (k∈Z)时,函数f(x)取得最大值,其最大值为
(k∈Z)时,函数f(x)取得最大值,其最大值为 .
.
(2)∵f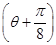 =
=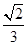 ,
,
∴ sin
sin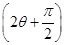 =
=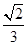 ,
,
∴cos 2θ=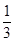 .
.
∵θ为锐角,即0<θ<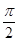 ,∴0<2θ<π,
,∴0<2θ<π,
∴sin 2θ=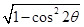 =
=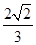 ,
,
∴tan 2θ=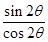 =2
=2 ,
,
∴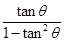 =2
=2 ,
,
∴ tan2θ+tan θ-
tan2θ+tan θ- =0,
=0,
∴( tan θ-1)(tan θ+
tan θ-1)(tan θ+ )=0,
)=0,
∴tan θ=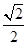 或tan θ=-
或tan θ=- (不合题意,舍去),∴tan θ=
(不合题意,舍去),∴tan θ=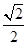 .
.
=sin 2x+cos 2x
=

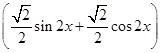
=
 sin
sin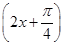 .
.∴当2x+
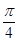 =2kπ+
=2kπ+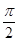 (k∈Z),即x=kπ+
(k∈Z),即x=kπ+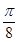 (k∈Z)时,函数f(x)取得最大值,其最大值为
(k∈Z)时,函数f(x)取得最大值,其最大值为 .
.(2)∵f
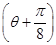 =
=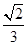 ,
,∴
 sin
sin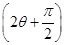 =
=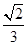 ,
,∴cos 2θ=
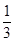 .
.∵θ为锐角,即0<θ<
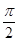 ,∴0<2θ<π,
,∴0<2θ<π,∴sin 2θ=
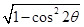 =
=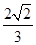 ,
,∴tan 2θ=
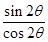 =2
=2 ,
,∴
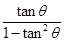 =2
=2 ,
,∴
 tan2θ+tan θ-
tan2θ+tan θ- =0,
=0,∴(
 tan θ-1)(tan θ+
tan θ-1)(tan θ+ )=0,
)=0,∴tan θ=
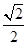 或tan θ=-
或tan θ=- (不合题意,舍去),∴tan θ=
(不合题意,舍去),∴tan θ=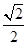 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.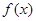 的最大值,并写出
的最大值,并写出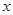 的取值集合;
的取值集合;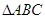 中,角
中,角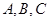 的对边分别为
的对边分别为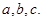 若
若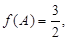
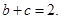 求实数
求实数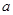 的最小值.
的最小值.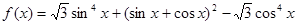 .
.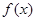 的最小值及取最小值时
的最小值及取最小值时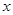 的集合;
的集合;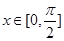 时的值域;
时的值域;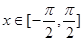 时的单调递减区间.
时的单调递减区间.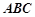 中,角
中,角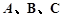 的对边分别为
的对边分别为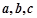 ,
, .
.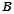 的大小;
的大小;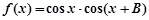
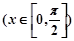 的值域
的值域 )来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( )
)来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( )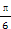 ),1),b=(4,4cosα-
),1),b=(4,4cosα-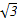 ),若a⊥b,则sin(α+
),若a⊥b,则sin(α+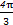 )=( )
)=( )

 sin x,sin x),b=(cos x,sin x),x∈
sin x,sin x),b=(cos x,sin x),x∈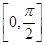 .
.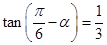 ,则
,则 的值为 .
的值为 .
 的值域为 .
的值域为 .