题目内容
【题目】进入冬季以来，我国北方地区的雾霾天气持续出现，极大的影响了人们的健康和出行，我市环保局对该市2015年进行为期一年的空气质量监测，得到每天的空气质量指数，从中随机抽取50个作为样本进行分析报告，样本数据分组区间为（5，15]，（15，25]，（25，35]，（35，45]，由此得到样本的空气质量指数频率分布直方图，如图．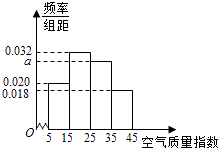
（1）求a的值；
（2）如果空气质量指数不超过15，就认定空气质量为“特优等级”，则从今年的监测数据中随机抽取3天的数值，其中达到“特优等级”的天数为X．求X的分布列和数学期望．
【答案】
（1）解：由频率分布直方图中小矩形面积之和为1，
得：（0.02+0.032+a+0.018）×10=1，
解得a=0.03．
（2）解：利用样本估计总体，该年度空所质量指数在（5，15]内为“特优等级”，
且指数达到“特优等级”的概率为0.2，
则X的取值为0，1，2，3，且X～B（3， 
），
P（X=0）= 
= 
，
P（X=1）= 
= 
，
P（X=2）= 
= 
，
P（X=3）= 
，
∴X的分布列为：
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴EX=0× +1× +2× +3× 
= 
【解析】（1）由频率分布直方图中小矩形面积之和为1，由此能求出a．（2）由已知得X的取值为0，1，2，3，且X～B（3， ），由此能求出X的分布列和EX．
【考点精析】认真审题，首先需要了解频率分布直方图(频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息)，还要掌握离散型随机变量及其分布列(在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列)的相关知识才是答题的关键．
