题目内容
【题目】已知x，y∈R且满足不等式组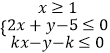 
，当k=1时，不等式组所表示的平面区域的面积为 ， 若目标函数z=3x+y的最大值为7，则k的值为 ．
【答案】
；2
【解析】解：若k=1，则不等式组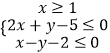 
对应的平面区域如图：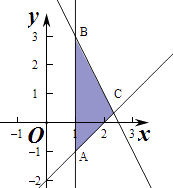 
则A（1，﹣1），B（1，3），
由 
得 
，即C（ 
， 
），
不等式组所表示的平面区域的面积为S= 
×4×（ ﹣1）=2× 
= ，
由z=3x+y得y=﹣3x+z，
平移直线y=﹣3x+z，则由图象可知当直线y=﹣3x+z经过点C时，直线y=﹣3x+z的截距最大，此时z最大，为3x+y=7
由 
，解得 
，即A（2，1），
此时A在kx﹣y﹣k﹣1=0上，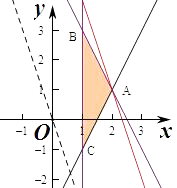
则2k﹣1﹣k﹣1=0，
得k=2．
所以答案是： ；2；
【题目】某中学调查了某班全部50名同学参加书法社团和演讲社团的情况，数据如下表：（单位：人）
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 6 |
未参加演讲社团 | 6 | 30 |
（I）从该班随机选1名同学，求该同学至少参加上述一个社团的概率；
（II）在既参加书法社团又参加演讲社团的8名同学中，有5名男同学A1，A2，A3，A4，A5，3名女同学B1，B2，B3，现从这5名男同学和3名女同学中各随机选1人，求A1被选中且B1未被选中的概率．
【题目】设AB=6，在线段AB上任取两点C、D（端点A、B除外），将线段AB分成三条线段AC、CD、DB．
（1）若分成的三条线段的长度均为正整数，求这三条线段可以构成三角形（称为事件A）的概率；
（2）若分成的三条线段的长度均为正实数，求这三条线段可以构成三角形（称为事件B）的概率；
（3）根据以下用计算机所产生的20组随机数，试用随机数模拟的方法，来近似计算（2）中事件B的概率， 20组随机数如下：
组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
X | 0.52 | 0.36 | 0.58 | 0.73 | 0.41 | 0.6 | 0.05 | 0.32 | 0.38 | 0.73 |
Y | 0.76 | 0.39 | 0.37 | 0.01 | 0.04 | 0.28 | 0.03 | 0.15 | 0.14 | 0.86 |
组别 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
X | 0.67 | 0.47 | 0.58 | 0.21 | 0.54 | 0.64 | 0.36 | 0.35 | 0.95 | 0.14 |
Y | 0.41 | 0.54 | 0.51 | 0.37 | 0.31 | 0.23 | 0.56 | 0.89 | 0.17 | 0.03 |
（X和Y都是0～1之间的均匀随机数）
