题目内容
4.x=1是函数f(x)=ex-m-ln(2x)的极值点,则m的值为1.分析 求出f′(x),由题意可知f'(1)=0,由此可求m,验证m的值,x=1是函数的极值点.
解答 解:∵f(x)=ex-m-ln(2x),
∴f′(x)=ex-m-$\frac{1}{x}$,
由x=1是函数f(x)的极值点得f′(1)=0,
即e1-m-1=0,∴m=1.
于是f(x)=ex-1-ln(2x),f′(x)=ex-1-$\frac{1}{x}$,
由x>1知 f′(x)在x∈(0,+∞)上单调递增,0<x<1且f′(1)<0,函数是减函数,
∴x=1是f′(x)=0的唯一零点.也是函数f(x)=ex-m-ln(2x)的极值点.
故答案为:1.
点评 本题考查利用导数研究函数的极值、单调性,考查学生灵活运用知识分析解决问题的能力.

练习册系列答案
相关题目
16.已知△ABC中,a,b,c分别为角A,B,C的对应边,A=30°,B=45°,a=7,则边长b为( )
| A. | $\frac{7}{2}\sqrt{2}$ | B. | $14\sqrt{2}$ | C. | $7\sqrt{2}$ | D. | $\frac{7}{3}\sqrt{6}$ |
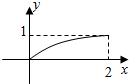 已知函数y=f(x)是定义在区间[-2,2]上的奇函数,当0≤x≤2时的图象如图所示,则y=f(x)的值域为[-1,1].
已知函数y=f(x)是定义在区间[-2,2]上的奇函数,当0≤x≤2时的图象如图所示,则y=f(x)的值域为[-1,1].