题目内容
(本小题满分12分)如图 ,已知在四棱锥
,已知在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, ,
, 是
是 的中点,
的中点,  是线段
是线段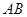 上的点.
上的点.

(I)当 是
是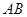 的中点时,求证:
的中点时,求证: 平面
平面 ;
;
(II)要使二面角 的大小为
的大小为 ,试确定
,试确定 点的位置.
点的位置.
 ,已知在四棱锥
,已知在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, ,
, 是
是 的中点,
的中点,  是线段
是线段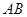 上的点.
上的点.
(I)当
 是
是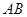 的中点时,求证:
的中点时,求证: 平面
平面 ;
;(II)要使二面角
 的大小为
的大小为 ,试确定
,试确定 点的位置.
点的位置.(I)只需证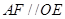 ;(II)
;(II)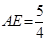 。
。
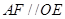 ;(II)
;(II)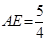 。
。试题分析:【法一】(I)证明:如图,取
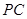 的中点
的中点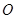 ,连接
,连接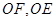 .
.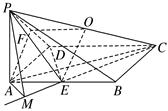
由已知得
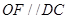 且
且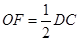 ,
,又
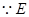 是
是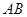 的中点,则
的中点,则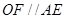 且
且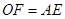 ,
,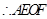 是平行四边形, ………………
是平行四边形, ………………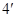
∴
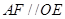
又
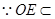 平面
平面 ,
,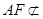 平面
平面
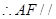 平面
平面 ………………………
………………………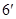
(II)如图,作
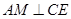 交
交 的延长线于
的延长线于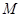 .
.连接
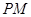 ,由三垂线定理得
,由三垂线定理得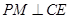 ,
,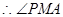 是二面角
是二面角 的平面角.即
的平面角.即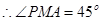 …………………
…………………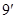
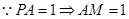 ,设
,设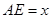 ,
,由
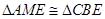 可得
可得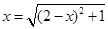
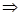
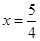
故,要使要使二面角
 的大小为
的大小为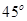 ,只需
,只需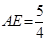 ………………
………………
【法二】(I)由已知,
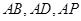 两两垂直,分别以它们所在直线为
两两垂直,分别以它们所在直线为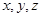 轴建立空间直角坐标系
轴建立空间直角坐标系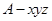 .
.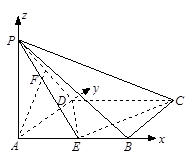
则
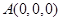 ,
,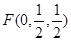 ,则
,则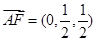 ………………
………………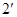
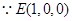 ,
,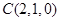 ,
,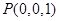 ,
,设平面
 的法向量为
的法向量为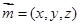
则
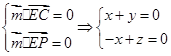 ,
,令
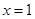 得
得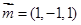 ………………………………………
………………………………………
由
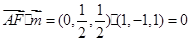 ,得
,得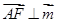
又
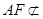 平面
平面 ,故
,故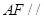 平面
平面 …………………
…………………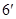
(II)由已知可得平面
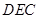 的一个法向量为
的一个法向量为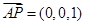 ,
,设
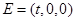 ,设平面
,设平面 的法向量为
的法向量为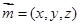
则
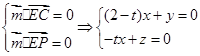 ,令
,令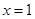 得
得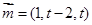 ……………
……………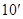
由
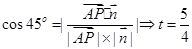 ,
, 故,要使要使二面角
 的大小为
的大小为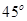 ,只需
,只需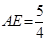 ……………
……………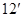
点评:综合法求二面角,往往需要作出平面角,这是几何中一大难点,而用向量法求解二面角无需作出二面角的平面角,只需求出平面的法向量,经过简单运算即可,从而体现了空间向量的巨大作用.二面角的向量求法: ①若AB、CD分别是二面
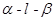 的两个半平面内与棱
的两个半平面内与棱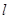 垂直的异面直线,则二面角的大小就是向量
垂直的异面直线,则二面角的大小就是向量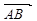 与
与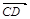 的夹角或补角; ②设
的夹角或补角; ②设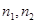 分别是二面角
分别是二面角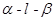 的两个面α,β的法向量,则向量
的两个面α,β的法向量,则向量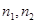 的夹角(或其补角)的大小就是二面角的平面角的大小。
的夹角(或其补角)的大小就是二面角的平面角的大小。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 点
点 上,过点
上,过点 做
做 //
// 将
将 的位置(
的位置( ),
), .
.
 (II)试问:当点
(II)试问:当点 的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
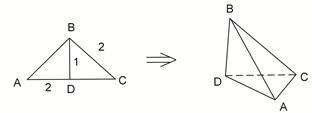
的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.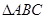 中,
中,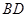 为
为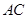 边上的高,
边上的高,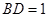 ,
,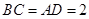 ,沿
,沿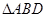 翻折,使得
翻折,使得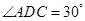 ,得到几何体
,得到几何体 。
。
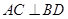 ;
;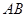 与平面
与平面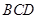 所成角的正切值。
所成角的正切值。 中,其中
中,其中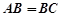 ,
,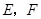 分别是
分别是 ,
, 的中点,则以下结论中
的中点,则以下结论中
 与
与 垂直; ②
垂直; ② ;
; 所成角为
所成角为 ; ④
; ④
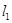 、
、 、
、 是空间三条不同的直线,下列命题中正确的是( )
是空间三条不同的直线,下列命题中正确的是( ) ,
, .则
.则 .
. ,
, .则
.则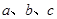 及平面
及平面 ,它们具备下列哪组条件时,有
,它们具备下列哪组条件时,有 成立( )
成立( )

 和
和
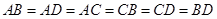 ,
,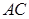 与
与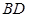 所成角为
所成角为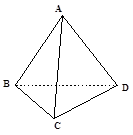
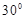
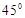
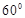
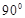
 ,其中m∥n,那么在平面
,其中m∥n,那么在平面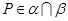 且
且 ,则
,则 ;
; 确定一个平面;
确定一个平面; ,则直线
,则直线 与
与 能够确定一个平面;
能够确定一个平面;  且
且 ,则
,则 .
.