Question

【题目】在直角坐标平面内，以坐标原点O为极点， 轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程是，直线的参数方程是（为参数）．

（1）求直线的普通方程和曲线的直角坐标方程；

（2）求曲线上的点到直线的距离的最大值．

Answer 1

【答案】（1）；（2）

【解析】试题分析：把参数方程化为普通方程只需削去参数，把极坐标方程化为直角坐标方程需要利用公式 ；求圆上一点到直线的距离的最大值可借助圆的参数方程巧设点，借助三角函数求最值，也可求圆心到直线的距离减去半径.

试题解析：（1）直线消得：，直线的普通方程为，

曲线的极坐标方程化为，

化直角坐标方程为，即.

（2）在曲线上任取一点，可设其坐标为，

到直线的距离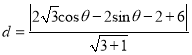

，

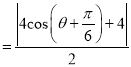
当且仅当时等号成立，

曲线上的点到直线的距离最大值为.