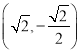题目内容
【题目】如图1是定义在R上的二次函数f(x)的部分图像,图2是函数![]() 的部分图像。
的部分图像。
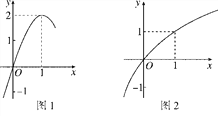
(Ⅰ) 分别求出函数![]() 和
和![]() 的解析式;
的解析式;
(Ⅱ)如果函数![]() 在区间
在区间![]() 上是单调递减函数,求
上是单调递减函数,求![]() 的取值范围。
的取值范围。
【答案】(1) ![]() ,
,![]() ;(2)
;(2) ![]()
【解析】试题分析:(1)由题图1得,二次函数f(x)的顶点坐标可设函数的顶点式f(x)=a(x﹣1)2+2,又函数f(x)的图象过点(0,0),求出a,得f(x)的解析式.由题图2得,函数g(x)=loga(x+b)的图象过点(0,0)和(1,1),将点的坐标代入列出关于a,b的方程组,解得a,b.最后写出g(x)的解析式即可;
(2)由(1)得y=g(f(x))=log2(﹣2x2+4x+1)是由y=log2t和t=﹣2x2+4x+1复合而成的函数,利用复合函数的单调性研究此函数的单调性,从而得出满足条件的m的取值范围.
试题解析:
(Ⅰ) f(x)=a(x-1)2+2.又函数f(x).的图像过点(0,0),故a=-2,
整理得f(x)=-2x2+4x.
由题图2得,函数g(x)=loga(x+b)的图像过点(0,0)和(1,1),
故有![]() ∴
∴![]()
∴g(x)=log2(x+1).
(Ⅱ)由(Ⅰ) 得y=g[f(x)]=log2(-2x2+4x+1)是由
y=log2t和t=-2x2+4x+1复合而成的函数,
而y=log2t在定义域上单调递增,
要使函数y=g[f(x)]在区间[1,m)上单调递减,
必须使t=-2x2+4x+1在区间[1,m)上单调递减,且有t>0恒成立.
又∵其对称轴x=![]() =1,且由t=0,得x=
=1,且由t=0,得x=![]() .
.
故1<m≤![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目