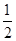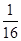题目内容
设函数f(x)=log2(ax-bx),且f(1)=1,f(2)=log212
(1)求a,b的值.
(2)当x∈[1,2]时,求f(x)的最大值.
(3)p为何值时,函数g(x)=ax-bx+p与x轴有两个交点.
(1)求a,b的值.
(2)当x∈[1,2]时,求f(x)的最大值.
(3)p为何值时,函数g(x)=ax-bx+p与x轴有两个交点.
(1)由题意,列方程组
求得a=4,b=2..(4分)
(2)由(1)知f(x)=log2(4x-2x)=log2[(2x-
)2-
]
∵1≤x≤2∴2≤2x≤4(2分)
故t=(2x-
)2-
在[1,2]上单调递减
∴f(x)的最大值=f(2)=log212(2分)
(3)令g(x)=4x-2x+p=0,则4x-2x+p=0有两个不同解.
令t=2x则t>0故t2-t+p=0有两个不同正根(2分)
即△=1-4p>0且p>0,(2分)
解得0<p<1/4.(2分)
|
求得a=4,b=2..(4分)
(2)由(1)知f(x)=log2(4x-2x)=log2[(2x-
| 1 |
| 2 |
| 1 |
| 4 |
∵1≤x≤2∴2≤2x≤4(2分)
故t=(2x-
| 1 |
| 2 |
| 1 |
| 4 |
∴f(x)的最大值=f(2)=log212(2分)
(3)令g(x)=4x-2x+p=0,则4x-2x+p=0有两个不同解.
令t=2x则t>0故t2-t+p=0有两个不同正根(2分)
即△=1-4p>0且p>0,(2分)
解得0<p<1/4.(2分)

练习册系列答案
相关题目

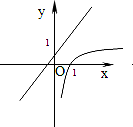
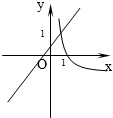
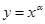 的图象经过点
的图象经过点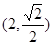 ,则
,则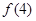 的值等于( ).
的值等于( ).