题目内容
已知[x]表示不超过x的最大整数,则[log21]+[log22]+[log23]+…[log22009]的值为( )
| A.18054 | B.18044 | C.17954 | D.17944 |
根据题意,当2k≤n<2k+1时,[log2n]=k(k∈N),
于是[log21]+[log22]+[log23]+…[log22009]
=0+(1+1)+(2+2+2+2)+…+(10+10+…+10)
=0•(21-20)+1•(22-21)+2•(23-22)+…+9•(210-29)+10•(2009-210+1)=18054.
故选:A.
于是[log21]+[log22]+[log23]+…[log22009]
=0+(1+1)+(2+2+2+2)+…+(10+10+…+10)
=0•(21-20)+1•(22-21)+2•(23-22)+…+9•(210-29)+10•(2009-210+1)=18054.
故选:A.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目

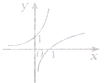
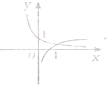
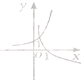
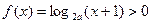 ,则a的取值范围是( )
,则a的取值范围是( ) 


