题目内容
15.已知函数$f(x)=\frac{{\sqrt{|x|}}}{e^x}({x∈R})$,若关于x的方程f2(x)-mf(x)+m-1=0恰好有4个不相等的实数根,则实数m的取值范围为( )| A. | $({1\;,\;\frac{{\sqrt{2e}}}{2e}+1})$ | B. | $({0\;,\;\frac{{\sqrt{2e}}}{2e}})$ | C. | $({1\;,\;\frac{1}{e}+1})$ | D. | $({\frac{{\sqrt{2e}}}{2e}\;,\;1})$ |
分析 求函数的导数,判断函数的取值情况,设m=f(x),利用换元法,将方程转化为一元二次方程,利用根的分布建立条件关系即可得到结论.
解答 解:化简可得f(x)=$\left\{\begin{array}{l}{\frac{\sqrt{x}}{{e}^{x},}}&{x≥0}\\{\frac{\sqrt{-x}}{{e}^{x}},}&{x<0}\end{array}\right.$,
当x>0时,f(x)≥0,f′(x)=$\frac{(\sqrt{x})′{e}^{x}-\sqrt{x}•{e}^{x}}{({e}^{x})^{2}}$=$\frac{\frac{1}{2\sqrt{x}}-\sqrt{x}}{{e}^{x}}$=$\frac{1-2x}{2\sqrt{x}{e}^{x}}$,
当0<x<$\frac{1}{2}$时,f′(x)>0,当x>$\frac{1}{2}$时,f′(x)<0,
故当x=$\frac{1}{2}$时,函数f(x)有极大值f($\frac{1}{2}$)=$\frac{\sqrt{\frac{1}{2}}}{{e}^{\frac{1}{2}}}$=$\frac{\frac{\sqrt{2}}{2}}{\sqrt{e}}$=$\frac{\sqrt{2}}{2\sqrt{e}}$=$\frac{\sqrt{2e}}{2e}$;
当x<0时,f′(x)=$\frac{-\frac{1}{2\sqrt{-x}}•{e}^{x}-\sqrt{-x}•{e}^{x}}{({e}^{x})^{2}}$=$\frac{-1+2x}{2\sqrt{-x}•{e}^{x}}$<0,f(x)为减函数,
作出函数f(x)对应的图象如图:
∴函数f(x)在(0,+∞)上有一个最大值为f($\frac{1}{2}$)=$\frac{\sqrt{2e}}{2e}$;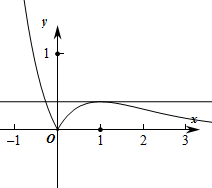
设t=f(x),
当t>$\frac{\sqrt{2e}}{2e}$时,方程t=f(x)有1个解,
当t=$\frac{\sqrt{2e}}{2e}$时,方程t=f(x)有2个解,
当0<t<$\frac{\sqrt{2e}}{2e}$时,方程t=f(x)有3个解,
当t=0时,方程t=f(x)有1个解,
当t<0时,方程m=f(x)有0个解,
则方程f2(x)-mf(x)+m-1=0等价为t2-mt+m-1=0,
等价为方程t2-mt+m-1=(t-1)[t-(m-1)]=0有两个不同的根t=1,或t=m-1,
当t=1时,方程t=f(x)有1个解,
要使关于x的方程f2(x)-mf(x)+m-1=0恰好有4个不相等的实数根,
则t=m-1∈(0,$\frac{\sqrt{2e}}{2e}$),
即0<m-1<$\frac{\sqrt{2e}}{2e}$,解得1<m<$\frac{\sqrt{2e}}{2e}$+1,
则m的取值范围是(1,$\frac{\sqrt{2e}}{2e}$+1)
故选:A
点评 本题考查了根的存在性及根的个数的判断,考查了利用函数的导函数分析函数的单调性,考查了学生分析问题和解决问题的能力,利用换元法转化为一元二次方程,是解决本题的关键.


| A. | 80 dm3 | B. | 88 dm3 | C. | 96 dm3 | D. | 120 dm3 |
| A. | -2 | B. | 0 | C. | 1 | D. | -2 |
| A. | (1,2) | B. | (-1,-2) | C. | (1,1) | D. | (-1,-1) |
| A. | 4 | B. | 2 | C. | $\frac{{\sqrt{2}+\sqrt{6}}}{2}$ | D. | $\sqrt{2}$ |
 如图,A,B,C是椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC.
如图,A,B,C是椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC.