题目内容
设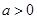 ,函数
,函数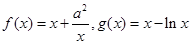 ,若对任意的
,若对任意的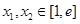 ,都有
,都有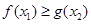 成立,则实数
成立,则实数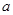 的取值范围为 .
的取值范围为 .
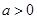 ,函数
,函数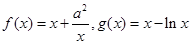 ,若对任意的
,若对任意的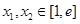 ,都有
,都有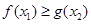 成立,则实数
成立,则实数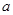 的取值范围为 .
的取值范围为 . 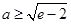
解:求导函数,可得g′(x)=1-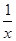 ,x∈[1,e],g′(x)≥0,
,x∈[1,e],g′(x)≥0,
∴g(x)max=g(e)=e-1,f′(x)=1-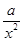 ,令f'(x)=0,
,令f'(x)=0,
∵a>0,x=±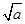
当0<a<1,f(x)在[1,e]上单调增,
∴f(x)min=f(1)=1+a≥e-1,∴a≥e-2;
当1≤a≤e2,f(x)在[1,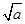 ]上单调减,f(x)在[
]上单调减,f(x)在[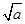 ,e]上单调增,
,e]上单调增,
∴f(x)min=f( a )=2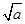 ≥e-1 恒成立;
≥e-1 恒成立;
当a>e2时 f(x)在[1,e]上单调减,
∴f(x)min=f(e)=e+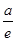 ≥e-1 恒成立
≥e-1 恒成立
综上a≥e-2
故答案为:[e-2,+∞)
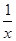 ,x∈[1,e],g′(x)≥0,
,x∈[1,e],g′(x)≥0,∴g(x)max=g(e)=e-1,f′(x)=1-
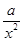 ,令f'(x)=0,
,令f'(x)=0,∵a>0,x=±
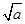
当0<a<1,f(x)在[1,e]上单调增,
∴f(x)min=f(1)=1+a≥e-1,∴a≥e-2;
当1≤a≤e2,f(x)在[1,
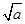 ]上单调减,f(x)在[
]上单调减,f(x)在[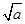 ,e]上单调增,
,e]上单调增,∴f(x)min=f( a )=2
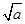 ≥e-1 恒成立;
≥e-1 恒成立;当a>e2时 f(x)在[1,e]上单调减,
∴f(x)min=f(e)=e+
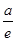 ≥e-1 恒成立
≥e-1 恒成立综上a≥e-2
故答案为:[e-2,+∞)

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
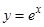 在点
在点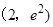 处的切线与两坐标轴所围成的三角形面积为( )
处的切线与两坐标轴所围成的三角形面积为( ) 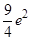
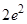
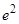
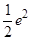
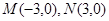 ,圆
,圆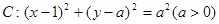 ,过
,过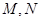 与圆
与圆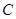 相切的两直线相交于点
相切的两直线相交于点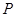 ,则点
,则点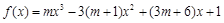 ,其中
,其中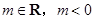 ,
,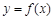 在(2,–3)处的切线方程;
在(2,–3)处的切线方程;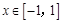 时,函数
时,函数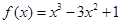 在
在 _____ 处取得极小值
_____ 处取得极小值 与
与 ,
,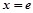 及
及 轴围成图形的面积是( )
轴围成图形的面积是( )

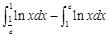

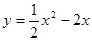 在点(1 ,
在点(1 ,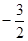 )处切线的斜率为
)处切线的斜率为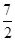
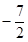
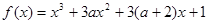 有极大值又有极小值,则
有极大值又有极小值,则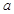 取值范围是____
取值范围是____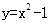 ,直线
,直线 和
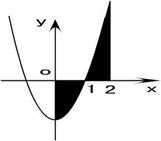
和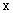 轴围城的封闭图形(阴影)的面积为( )
轴围城的封闭图形(阴影)的面积为( )