题目内容
.(本题满分15分)已知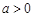 ,函数
,函数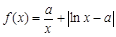 ,
,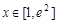 .
.
(Ⅰ)当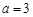 时,求曲线
时,求曲线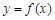 在点
在点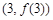 处的切线方程;
处的切线方程;
(Ⅱ)若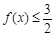 恒成立,求实数
恒成立,求实数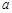 的取值范围.
的取值范围.
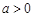 ,函数
,函数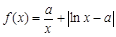 ,
,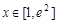 .
.(Ⅰ)当
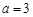 时,求曲线
时,求曲线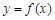 在点
在点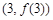 处的切线方程;
处的切线方程;(Ⅱ)若
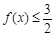 恒成立,求实数
恒成立,求实数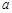 的取值范围.
的取值范围.(Ⅰ) .(Ⅱ)
.(Ⅱ)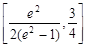
 .(Ⅱ)
.(Ⅱ)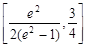
本试题主要是考查了导数的几何意义的运用,以及运用导数解决不等式的恒成立e问题的运用。
(1)由于导数值表示的就是曲线在该点的斜率,那么利用点的坐标好斜率,得到切线方程的问题。
(2)要是不等式恒成立,则需要求解函数f(x)的最大值即可,因此需要对参数a进行分类讨论研究其最值。
解:(Ⅰ)当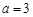 时,
时, ,(2分)
,(2分)
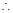
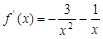 ,
,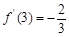 ,(4分)
,(4分)
又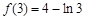 ,
,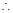 曲线
曲线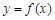 在点
在点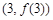 处的切线方程为:
处的切线方程为:
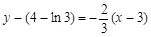 ,即:
,即: .(6分)
.(6分)
(Ⅱ)由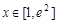 得
得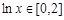
①当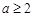 时
时
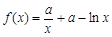 ,
,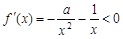 ,∴
,∴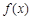 在
在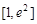 上递减,
上递减,
∴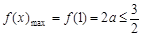 ,∴
,∴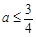 ,此时
,此时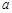 不存在;( 8分)
不存在;( 8分)
②当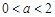 时
时
若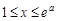 时,
时,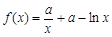 由①得
由①得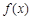 在
在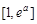 上递减,
上递减,
∴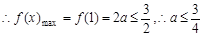 ,此时
,此时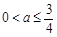 (9分)
(9分)
若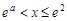 时
时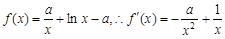
令 得
得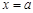 ,又
,又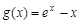 在
在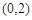 递增,故
递增,故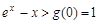
∴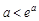 ,当
,当
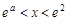 时
时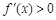 ,∴
,∴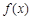 在
在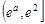 递增,(12分)
递增,(12分)
∴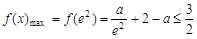
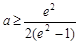 ,
,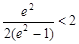 ,∴
,∴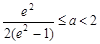 ,(13分)
,(13分)
又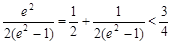 , ∴
, ∴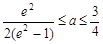
综上知,实数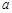 的取值范围
的取值范围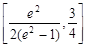 (15分)
(15分)
(1)由于导数值表示的就是曲线在该点的斜率,那么利用点的坐标好斜率,得到切线方程的问题。
(2)要是不等式恒成立,则需要求解函数f(x)的最大值即可,因此需要对参数a进行分类讨论研究其最值。
解:(Ⅰ)当
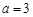 时,
时, ,(2分)
,(2分)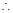
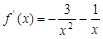 ,
,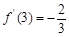 ,(4分)
,(4分)又
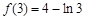 ,
, 曲线
曲线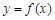 在点
在点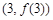 处的切线方程为:
处的切线方程为: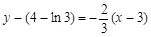 ,即:
,即: .(6分)
.(6分)(Ⅱ)由
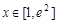 得
得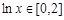
①当
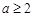 时
时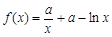 ,
,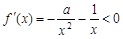 ,∴
,∴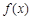 在
在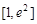 上递减,
上递减,∴
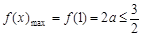 ,∴
,∴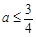 ,此时
,此时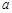 不存在;( 8分)
不存在;( 8分)②当
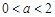 时
时若
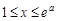 时,
时,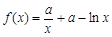 由①得
由①得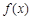 在
在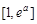 上递减,
上递减,∴
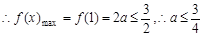 ,此时
,此时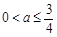 (9分)
(9分)若
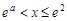 时
时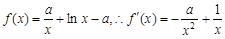
令
 得
得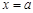 ,又
,又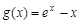 在
在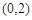 递增,故
递增,故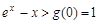
∴
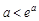 ,当
,当
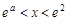 时
时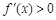 ,∴
,∴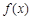 在
在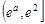 递增,(12分)
递增,(12分)∴
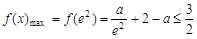
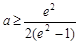 ,
,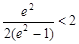 ,∴
,∴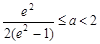 ,(13分)
,(13分)又
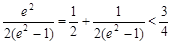 , ∴
, ∴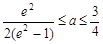
综上知,实数
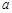 的取值范围
的取值范围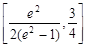 (15分)
(15分)
练习册系列答案
相关题目
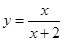 在点
在点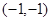 处的切线方程是
处的切线方程是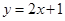
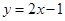
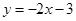
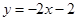
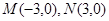 ,圆
,圆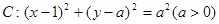 ,过
,过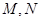 与圆
与圆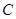 相切的两直线相交于点
相切的两直线相交于点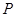 ,则点
,则点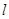 是曲线
是曲线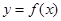 在
在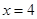 处的切线,则
处的切线,则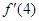 =
= 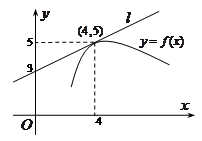
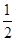
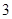
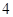
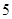
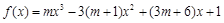 ,其中
,其中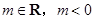 ,
,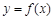 在(2,–3)处的切线方程;
在(2,–3)处的切线方程;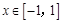 时,函数
时,函数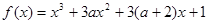 有极大值又有极小值,则
有极大值又有极小值,则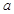 取值范围是____
取值范围是____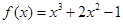 ,则
,则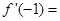 ( )
( )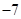
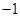
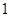
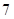
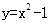 ,直线
,直线 和
和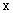 轴围城的封闭图形(阴影)的面积为( )
轴围城的封闭图形(阴影)的面积为( )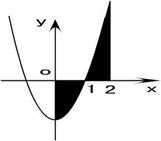
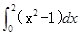
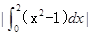
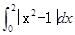
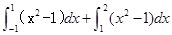
 ,则
,则 ( )
( )


