题目内容
设函数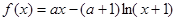
(Ⅰ)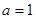 时,求
时,求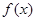 的单调区间;
的单调区间;
(Ⅱ)当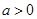 时,设
时,设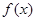 的最小值为
的最小值为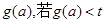 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
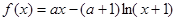
(Ⅰ)
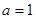 时,求
时,求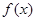 的单调区间;
的单调区间;(Ⅱ)当
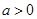 时,设
时,设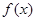 的最小值为
的最小值为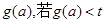 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.(Ⅰ)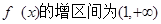
 (Ⅱ)
(Ⅱ) 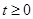 为所求.
为所求.
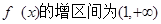
 (Ⅱ)
(Ⅱ) 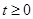 为所求.
为所求. (Ⅰ)利用导数法求得函数的单调区间,求解时需要注意函数的定义域;(Ⅱ)先利用已知把恒成立问题转化为求函数最值问题,然后利用导数法求出函数最值即可
(Ⅰ)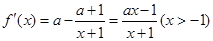 , ┄┄┄┄┄1分
, ┄┄┄┄┄1分
当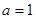 时,
时,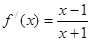 解
解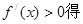
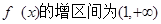
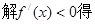
 ┄┄┄┄┄4分
┄┄┄┄┄4分
(Ⅱ)若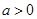 ,由
,由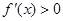 得
得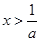 ,由
,由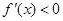 得
得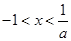 ,
,
所以函数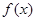 的减区间为
的减区间为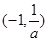 ,增区间为
,增区间为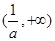 ;
;
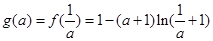 , ┄┄┄┄┄6分
, ┄┄┄┄┄6分
因为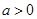 ,所以
,所以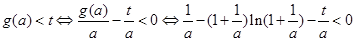 ,
,
令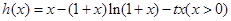 ,则
,则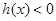 恒成立
恒成立
由于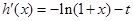 ,当
,当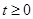 时,
时,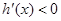 ,故函数
,故函数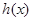 在
在 上是减函数,
上是减函数,
所以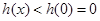 成立; ┄┄┄┄┄┄10分
成立; ┄┄┄┄┄┄10分
当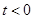 时,若
时,若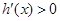 则
则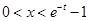 ,故函数
,故函数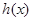 在
在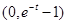 上是增函数,
上是增函数,
即对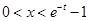 时,
时,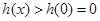 ,与题意不符;综上,
,与题意不符;综上,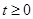 为所求
为所求
(Ⅰ)
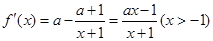 , ┄┄┄┄┄1分
, ┄┄┄┄┄1分当
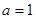 时,
时,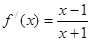 解
解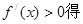
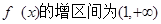
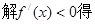
 ┄┄┄┄┄4分
┄┄┄┄┄4分(Ⅱ)若
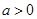 ,由
,由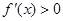 得
得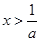 ,由
,由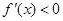 得
得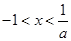 ,
,所以函数
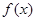 的减区间为
的减区间为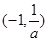 ,增区间为
,增区间为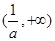 ;
;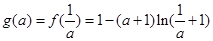 , ┄┄┄┄┄6分
, ┄┄┄┄┄6分因为
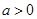 ,所以
,所以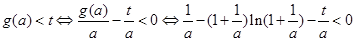 ,
,令
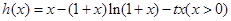 ,则
,则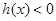 恒成立
恒成立由于
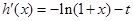 ,当
,当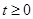 时,
时,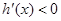 ,故函数
,故函数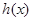 在
在 上是减函数,
上是减函数,所以
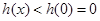 成立; ┄┄┄┄┄┄10分
成立; ┄┄┄┄┄┄10分当
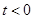 时,若
时,若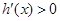 则
则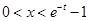 ,故函数
,故函数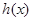 在
在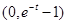 上是增函数,
上是增函数,即对
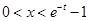 时,
时,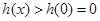 ,与题意不符;综上,
,与题意不符;综上,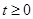 为所求
为所求
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
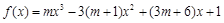 ,其中
,其中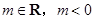 ,
,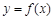 在(2,–3)处的切线方程;
在(2,–3)处的切线方程;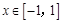 时,函数
时,函数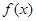 =
=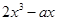 与
与 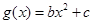 的图象都过点 P(2, 0), 且
的图象都过点 P(2, 0), 且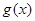 的表达式.
的表达式.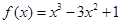 在
在 _____ 处取得极小值
_____ 处取得极小值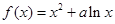 ,
,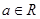 ,
,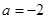 求
求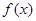 的极值
的极值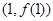 处的切线方程为
处的切线方程为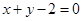 ,求实数
,求实数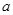 的值
的值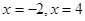 是函数
是函数 ,b=
,b= 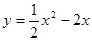 在点(1 ,
在点(1 ,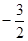 )处切线的斜率为
)处切线的斜率为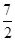
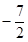
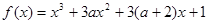 有极大值又有极小值,则
有极大值又有极小值,则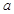 取值范围是____
取值范围是____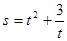 (
(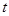 是时间,
是时间,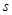 是位移),则物体在时刻
是位移),则物体在时刻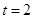 时的速度为( )
时的速度为( )