题目内容
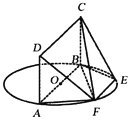
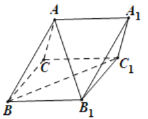
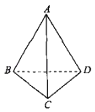
【题目】如图,在直棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 上的点,且
上的点,且![]() 平面
平面![]() .
.

(1)证明:![]() ;
;
(2)若![]() 为
为![]() 中点,求直线
中点,求直线![]() 与直线
与直线![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
解法1:(1)以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,建立空间直角坐标系
轴正方向,建立空间直角坐标系![]() .
.
设![]() ,
,![]() ,求出相应点的坐标,利用空间向量共线的定义求解即可;
,求出相应点的坐标,利用空间向量共线的定义求解即可;
(2)利用空间向量夹角公式进行求解即可.
解法2:(1)利用线面平行的性质定理,结合平行线公理进行证明即可;
(2)延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .利用平行四边形有判定定理、平行四边形的性质可以证明出
.利用平行四边形有判定定理、平行四边形的性质可以证明出![]() .所以
.所以![]() 直线
直线![]() 与直线
与直线![]() 所成角.利用余弦定理进行求解即可.
所成角.利用余弦定理进行求解即可.
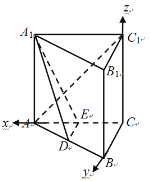
解法1:(1)如图,以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,建立空间直角坐标系
轴正方向,建立空间直角坐标系![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,所以
,所以![]() ,
,![]() 与
与![]() 共线.
共线.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)因为![]() 为
为![]() 中点,所以
中点,所以![]() 为
为![]() 中点,故
中点,故![]() ,于是
,于是![]() ,
,![]() .
.
所以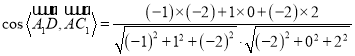
![]() ,
,
因此直线![]() 与直线
与直线![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
解法2:(1)因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() .
.
在直棱柱![]() 中,
中,![]() ,所以
,所以![]() .
.
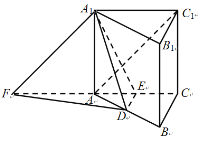
(2)延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .则
.则![]() ,
,![]() ,
,
四边形![]() 是平行四边形,所以
是平行四边形,所以![]() .故
.故![]() 直线
直线![]() 与直线
与直线![]() 所成角.
所成角.
设![]() ,则
,则![]() ,
,![]() .因为
.因为![]() 为
为![]() 中点,所以
中点,所以![]() 为
为![]() 中点,故
中点,故![]() .
.
因为![]() ,所以
,所以![]() ,因此
,因此![]() .
.
在![]() 中,
中,![]() .所以直线
.所以直线![]() 与直线
与直线![]() 所成角的余弦值为
所成角的余弦值为![]() .
.

 阅读快车系列答案
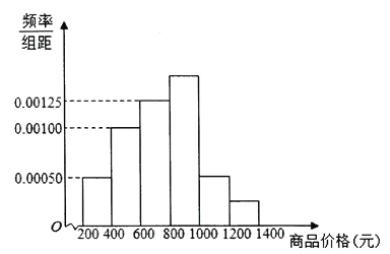
阅读快车系列答案【题目】2019年是扶贫的关键年,作为产业扶贫的电商扶贫将会迎来更多的政策或扶持.京东、阿里、拼多多、抖音、苏宁等互联网公司都纷纷加入电商扶贫.城乡各地区都展开农村电商培训,如对电商团队、物流企业、返乡创业群体、普通农户等进行培训.某部门组织A、B两个调查小组在开展电商培训之前先进行问卷调查,从获取的有效问卷中,针对25至55岁的人群,接比例随机抽取400份,进行数据统计,具体情况如下表:
A组统计结果 | B组统计结果 | |||
参加电商培训 | 不参加电商培训 | 参加电商培训 | 不参加电商培训 | |
| 50 | 25 | 45 | 20 |
| 35 | 43 | 30 | 32 |
| 20 | 60 | 20 | 20 |
(1)先用分层抽样的方法从400人中按“年龄是否达到45岁”抽出一个容量为80的样本,将“年龄达到45岁”的被抽个体分配到“参加电商培训”和“不参加电商培训”中去。
①这80人中“年龄达到45岁且参加电商培训”的人数;
②调查组从所抽取的“年龄达到45岁且参加电商培训”的人员中抽取3人,安排进入抖音公司参观学习,求这3人恰好是A组的人数X的分布列和数学期望;
(2)从统计数据可直观得出“参加电商培训与年龄(记作m岁)有关”的结论.请列出![]() 列联表,用独立性检验的方法,通过比较
列联表,用独立性检验的方法,通过比较![]() 的观测值的大小,判断年龄取35岁还是45岁时犯错误的概率哪一个更小?
的观测值的大小,判断年龄取35岁还是45岁时犯错误的概率哪一个更小?
(参考公式:![]() ,其中
,其中)
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.