题目内容
((本小题满分12分)
若函数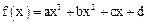 是奇函数,且
是奇函数,且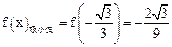 。
。
(1)求函数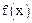 的解析式;
的解析式;
(2)求函数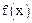 在
在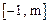
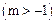 上的最大值;
上的最大值;
(3)设函数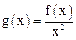 ,若不等式
,若不等式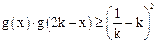 在
在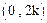 上恒成立,求实数k的取值范围.
上恒成立,求实数k的取值范围.
若函数
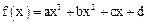 是奇函数,且
是奇函数,且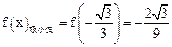 。
。(1)求函数
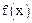 的解析式;
的解析式;(2)求函数
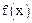 在
在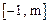
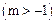 上的最大值;
上的最大值;(3)设函数
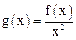 ,若不等式
,若不等式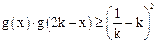 在
在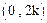 上恒成立,求实数k的取值范围.
上恒成立,求实数k的取值范围.解:(1)函数f(x)=ax3+bx2+cx+d是奇函数,则b=d=0,
∴f /(x)=3ax2+c,则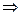
故f(x)=-x3+x;………………………………4分
(2)∵f /(x)=-3x2+1=-3(x+)(x-) ∴f(x)在(-∞,-),(,+∞)上是
增函数,在[-,]上是减函数,
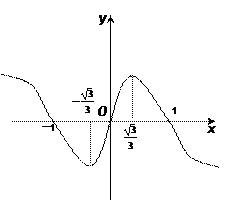
由f(x)=0解得x=±1,x=0,
如图所示, 当-1<m<0时,
f(x)max=f(-1)=0;当0≤m<时,f(x)max=f(m)=-m3+m,
当m≥时,f(x)max=f()=.
故f(x)max=.………………9分
(3)g(x)=(-x),令y=2k-x,则x、y∈R+,且2k=x+y≥2,
又令t=xy,则0<t≤k2,
故函数F(x)=g(x)·g(2k-x)=(-x)(-y)=+xy-
=+xy-=+t+2,t∈(0,k2]
当1-4k2≤0时,F(x)无最小值,不合
当1-4k2>0时,F(x)在(0,]上递减,在[,+∞)上递增,
且F(k2)=(-k)2,∴要F(k2)≥(-k)2恒成立,
必须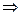 , 故实数k的取值范围是(0,)].…… 14分
, 故实数k的取值范围是(0,)].…… 14分
∴f /(x)=3ax2+c,则
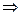
故f(x)=-x3+x;………………………………4分
(2)∵f /(x)=-3x2+1=-3(x+)(x-) ∴f(x)在(-∞,-),(,+∞)上是
增函数,在[-,]上是减函数,

由f(x)=0解得x=±1,x=0,
如图所示, 当-1<m<0时,
f(x)max=f(-1)=0;当0≤m<时,f(x)max=f(m)=-m3+m,
当m≥时,f(x)max=f()=.
故f(x)max=.………………9分
(3)g(x)=(-x),令y=2k-x,则x、y∈R+,且2k=x+y≥2,
又令t=xy,则0<t≤k2,
故函数F(x)=g(x)·g(2k-x)=(-x)(-y)=+xy-
=+xy-=+t+2,t∈(0,k2]
当1-4k2≤0时,F(x)无最小值,不合
当1-4k2>0时,F(x)在(0,]上递减,在[,+∞)上递增,
且F(k2)=(-k)2,∴要F(k2)≥(-k)2恒成立,
必须
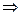 , 故实数k的取值范围是(0,)].…… 14分
, 故实数k的取值范围是(0,)].…… 14分略

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
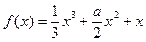 在
在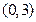 内有极值,求实数
内有极值,求实数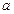 的范围。
的范围。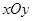 中,已知点P是函数
中,已知点P是函数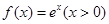 的图象上的动点,该图象在P处的切线
的图象上的动点,该图象在P处的切线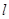 交y轴于点M,过点P作
交y轴于点M,过点P作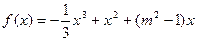 ,其中,
,其中,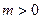
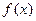 的极值和单调区间;;w
的极值和单调区间;;w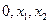 ,且
,且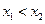 ,若对任意的
,若对任意的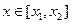 ,
,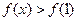 恒成立,求
恒成立,求 的取值范围
的取值范围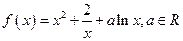
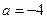 ,求函数
,求函数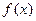 的单调区间;
的单调区间;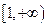 上单调递增,求实数
上单调递增,求实数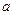 的取值范围
的取值范围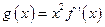 ,若
,若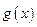 的最小值是
的最小值是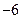 ,求函数
,求函数 ,
,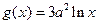 ,其中
,其中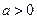 .若两曲线
.若两曲线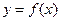 ,
,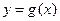 有公共点,且在该点处的切线相同.则
有公共点,且在该点处的切线相同.则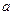 的值为 . (定义:
的值为 . (定义: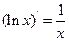 ).
).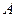 、
、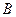 为椭圆
为椭圆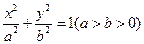 和双曲线
和双曲线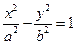 的公共顶点,
的公共顶点,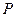 、
、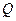 分别为双曲线和椭圆上不同于
分别为双曲线和椭圆上不同于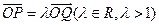 .设
.设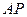 、
、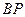 、
、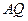 、
、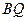 的斜率分别为
的斜率分别为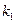 、
、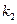 、
、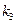 、
、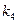 .
.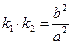 ;
;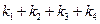 的值;
的值;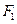 、
、 分别为双曲线和椭圆的右焦点,若
分别为双曲线和椭圆的右焦点,若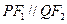 ,求
,求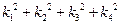 的值.
的值.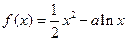 的图象在点
的图象在点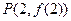 处的切线方程为
处的切线方程为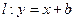
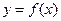 的表达式和切线
的表达式和切线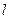 的方程;
的方程;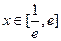 时(其中
时(其中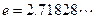 ),不等式
),不等式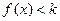 恒成立,求实数
恒成立,求实数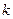 的取值范围.
的取值范围.