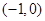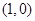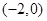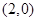题目内容
[2012·重庆高考]过抛物线y2=2x的焦点F作直线交抛物线于A,B两点,若|AB|=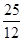 ,|AF|<|BF|,则|AF|=________.
,|AF|<|BF|,则|AF|=________.
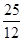 ,|AF|<|BF|,则|AF|=________.
,|AF|<|BF|,则|AF|=________.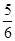
F点坐标为(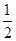 ,0),设A,B两点的横坐标为x1,x2.
,0),设A,B两点的横坐标为x1,x2.
因|AF|<|BF|,故直线AB不垂直于x轴.
设直线AB为y=k(x-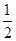 ),联立直线与抛物线的方程得k2x2-(k2+2)x+
),联立直线与抛物线的方程得k2x2-(k2+2)x+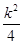 =0, ①
=0, ①
则x1+x2= .
.
又|AB|=x1+x2+1=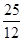 ,可解得k2=24,代入①式得12x2-13x+3=0,即(3x-1)(4x-3)=0.而|AF|<|BF|,所以x1=
,可解得k2=24,代入①式得12x2-13x+3=0,即(3x-1)(4x-3)=0.而|AF|<|BF|,所以x1=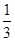 .
.
由抛物线的定义,得|AF|=x1+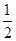 =
=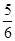 .
.
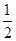 ,0),设A,B两点的横坐标为x1,x2.
,0),设A,B两点的横坐标为x1,x2.因|AF|<|BF|,故直线AB不垂直于x轴.
设直线AB为y=k(x-
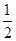 ),联立直线与抛物线的方程得k2x2-(k2+2)x+
),联立直线与抛物线的方程得k2x2-(k2+2)x+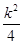 =0, ①
=0, ①则x1+x2=
 .
.又|AB|=x1+x2+1=
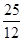 ,可解得k2=24,代入①式得12x2-13x+3=0,即(3x-1)(4x-3)=0.而|AF|<|BF|,所以x1=
,可解得k2=24,代入①式得12x2-13x+3=0,即(3x-1)(4x-3)=0.而|AF|<|BF|,所以x1=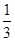 .
.由抛物线的定义,得|AF|=x1+
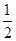 =
=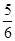 .
.
练习册系列答案
相关题目
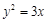 ,则抛物线的焦点坐标为 .
,则抛物线的焦点坐标为 . 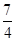
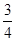

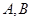 两点,若
两点,若 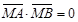 则
则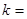
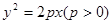 的焦点为F,过点F倾斜角为60°的直线l与抛物线C在第一、四象限分别交于A、B两点,则
的焦点为F,过点F倾斜角为60°的直线l与抛物线C在第一、四象限分别交于A、B两点,则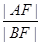 的值等于( )
的值等于( )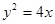 的焦点作一条直线交抛物线于
的焦点作一条直线交抛物线于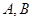 两点,若线段
两点,若线段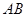 的中点
的中点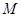 的横坐标为
的横坐标为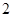 ,则
,则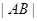 等于 .
等于 .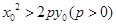 ,则称点
,则称点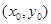 在抛物线C:
在抛物线C: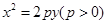 外.已知点
外.已知点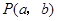 在抛物线C:
在抛物线C: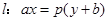 与抛物线C的位置关系是( )
与抛物线C的位置关系是( ) 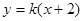 (k>0)与抛物线
(k>0)与抛物线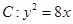 相交于
相交于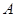 、
、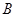 两点,
两点,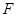 为
为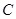 的焦点,若
的焦点,若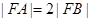 ,则k的值为 .
,则k的值为 .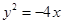 ,则它的焦点坐标为( )
,则它的焦点坐标为( )