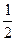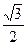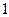题目内容
已知点 及圆
及圆 :
: .(Ⅰ)若直线
.(Ⅰ)若直线 过点
过点 且与圆心
且与圆心 的距离为1,求直线
的距离为1,求直线 的方程;(Ⅱ)设过点P的直线
的方程;(Ⅱ)设过点P的直线 与圆
与圆 交于
交于 、
、 两点,当
两点,当 时,求以线段
时,求以线段 为直径的圆
为直径的圆 的方程;(Ⅲ)设直线
的方程;(Ⅲ)设直线 与圆
与圆 交于
交于 ,
, 两点,是否存在实数
两点,是否存在实数 ,使得过点
,使得过点 的直线
的直线 垂直平分弦
垂直平分弦 ?若存在,求出实数
?若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 及圆
及圆 :
: .(Ⅰ)若直线
.(Ⅰ)若直线 过点
过点 且与圆心
且与圆心 的距离为1,求直线
的距离为1,求直线 的方程;(Ⅱ)设过点P的直线
的方程;(Ⅱ)设过点P的直线 与圆
与圆 交于
交于 、
、 两点,当
两点,当 时,求以线段
时,求以线段 为直径的圆
为直径的圆 的方程;(Ⅲ)设直线
的方程;(Ⅲ)设直线 与圆
与圆 交于
交于 ,
, 两点,是否存在实数
两点,是否存在实数 ,使得过点
,使得过点 的直线
的直线 垂直平分弦
垂直平分弦 ?若存在,求出实数
?若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(Ⅰ) 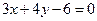 ,
,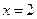 (Ⅱ)
(Ⅱ) 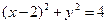 (Ⅲ)不存在
(Ⅲ)不存在
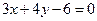 ,
,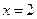 (Ⅱ)
(Ⅱ) 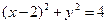 (Ⅲ)不存在
(Ⅲ)不存在:(Ⅰ)设直线 的斜率为
的斜率为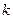 (
(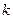 存在)则方程为
存在)则方程为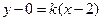 .
.
又圆C的圆心为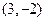 ,半径
,半径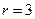 ,由
,由 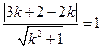 , 解得
, 解得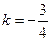 .
.
所以直线方程为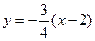 , 即
, 即 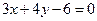 .
.
当 的斜率不存在时,
的斜率不存在时, 的方程为
的方程为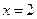 ,经验证
,经验证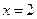 也满足条件
也满足条件
(Ⅱ)由于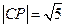 ,而弦心距
,而弦心距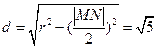 ,
,
所以
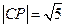 .所以
.所以 为
为 的中点.故以
的中点.故以 为直径的圆
为直径的圆 的方程为
的方程为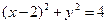
(Ⅲ)把直线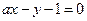 即
即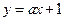 .代入圆
.代入圆 的方程,
的方程,
消去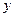 ,整理得
,整理得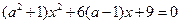 .由于直线
.由于直线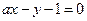 交圆
交圆 于
于 两点,故
两点,故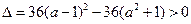 ,即
,即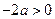 ,解得
,解得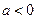 .
.
则实数 的取值范围是
的取值范围是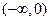 .设符合条件的实数
.设符合条件的实数 存在,
存在,
由于 垂直平分弦
垂直平分弦 ,故圆心
,故圆心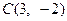 必在
必在 上.
上.
所以 的斜率
的斜率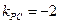 ,而
,而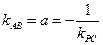 ,所以
,所以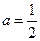 .由于
.由于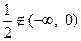 ,
,
故不存在实数 ,使得过点
,使得过点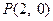 的直线
的直线 垂直平分弦
垂直平分弦 .
.
 的斜率为
的斜率为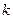 (
(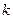 存在)则方程为
存在)则方程为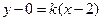 .
. 又圆C的圆心为
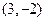 ,半径
,半径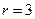 ,由
,由 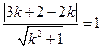 , 解得
, 解得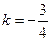 .
.所以直线方程为
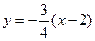 , 即
, 即 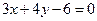 .
.当
 的斜率不存在时,
的斜率不存在时, 的方程为
的方程为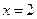 ,经验证
,经验证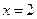 也满足条件
也满足条件 (Ⅱ)由于
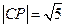 ,而弦心距
,而弦心距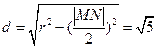 ,
,所以

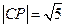 .所以
.所以 为
为 的中点.故以
的中点.故以 为直径的圆
为直径的圆 的方程为
的方程为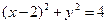
(Ⅲ)把直线
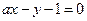 即
即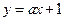 .代入圆
.代入圆 的方程,
的方程,消去
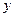 ,整理得
,整理得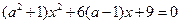 .由于直线
.由于直线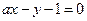 交圆
交圆 于
于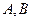 两点,故
两点,故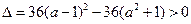 ,即
,即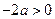 ,解得
,解得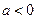 .
.则实数
 的取值范围是
的取值范围是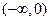 .设符合条件的实数
.设符合条件的实数 存在,
存在,由于
 垂直平分弦
垂直平分弦 ,故圆心
,故圆心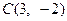 必在
必在 上.
上.所以
 的斜率
的斜率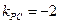 ,而
,而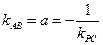 ,所以
,所以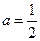 .由于
.由于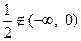 ,
,故不存在实数
 ,使得过点
,使得过点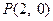 的直线
的直线 垂直平分弦
垂直平分弦 .
.
练习册系列答案
相关题目
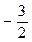 ),被圆O:x2+y2=25所截得的弦长为8,
),被圆O:x2+y2=25所截得的弦长为8, 是抛物线上的任意两点,
是抛物线上的任意两点, 是焦点,
是焦点, 是准线,若
是准线,若 三点共线,那么以弦
三点共线,那么以弦 为直径的圆与
为直径的圆与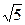
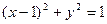 的圆心到直线
的圆心到直线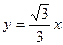 的距离是( )
的距离是( )