题目内容
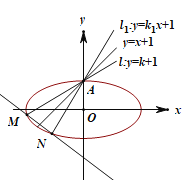
【题目】如图,直线![]() (
(![]() )关于直线
)关于直线![]() 对称的直线为
对称的直线为![]() ,直线
,直线![]() ,
,![]() 与椭圆
与椭圆![]() 分别交于点A,M和A,N,记直线
分别交于点A,M和A,N,记直线![]() 的斜率为
的斜率为![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 变化时,直线
变化时,直线![]() 是否恒过定点?若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
是否恒过定点?若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
【答案】(1)1;(2)当![]() 变化时,直线MN恒过定点
变化时,直线MN恒过定点![]() .
.
【解析】
(1)设直线![]() 上任意一点
上任意一点![]() 关于直线
关于直线![]() 对称点为
对称点为![]() ,利用
,利用![]() 与
与![]() 关于直线
关于直线![]() 对称可得关系式
对称可得关系式 ,代入斜率乘积即可得到
,代入斜率乘积即可得到![]() 的值;
的值;
(2)设出M,N的坐标,分别联立两直线方程与椭圆方程,求出M,N的坐标,进一步求出MN所在直线的斜率,写出直线方程的点斜式,整理后由直线系方程可得当k变化时,直线MN过定点![]() .
.
(1)设直线![]() 上任意一点
上任意一点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,
,
直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
据题意,得![]() ,∴
,∴![]() ①,
①,
![]() ,得
,得![]() ②,
②,
由①②,得 ,
,
∴![]() ;
;
(2)设点![]() ,
,![]() ,由
,由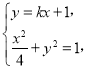 得
得![]() ,
,
∴![]() ,∴
,∴![]() .同理有
.同理有![]() ,
,![]() .又∵
.又∵![]() ,
,
∴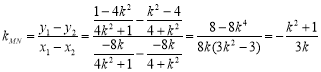 .∴
.∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴当![]() 变化时,直线MN恒过定点
变化时,直线MN恒过定点![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了调查高一学生在分班选科时是否选择物理科目与性别的关系,随机调查100名高一学生,得到![]() 列联表如下:由此得出的正确结论是( )
列联表如下:由此得出的正确结论是( )
选择物理 | 不选择物理 | 总计 | |
男 | 35 | 20 | 55 |
女 | 15 | 30 | 45 |
总计 | 50 | 50 | 100 |
附: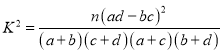
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A.在犯错误的概率不超过0.01的前提下,认为“选择物理与性别有关”
B.在犯错误的概率不超过0.01的前提下,认为“选择物理与性别无关”
C.有![]() 的把握认为“选择物理与性别有关”
的把握认为“选择物理与性别有关”
D.有![]() 的把握认为“选择物理与性别无关”
的把握认为“选择物理与性别无关”