题目内容
θ是第三象限角,方程x2+y 2sinθ=cosθ表示的曲线是( ).
| A.焦点在x轴上的椭圆 | B.焦点在y轴上的椭圆 |
| C.焦点在x轴上的双曲线 | D.焦点在y轴上的双曲线 |
D
解析试题分析:∵θ是第三象限角,∴sinθ<0, cosθ<0, ∴方程x2+y 2sinθ=cosθ化为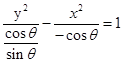 ,为焦点在y轴上的双曲线,故选D
,为焦点在y轴上的双曲线,故选D
考点:本题考查了圆锥曲线的方程
点评:熟练掌握圆锥曲线的方程特点是解决此类问题的关键,属基础题

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
一个顶点的坐标 ,焦距的一半为3的椭圆的标准方程是( )
,焦距的一半为3的椭圆的标准方程是( )
A. | B. | C. | D. |
若抛物线 的离心率
的离心率 ,则该抛物线准线方程是 ( )
,则该抛物线准线方程是 ( )
A. | B. | C. | D. |
等轴双曲线 的中心在原点,焦点在
的中心在原点,焦点在 轴上,
轴上, 与抛物线
与抛物线 的准线交于
的准线交于 两点,
两点,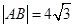 ;则
;则 的实轴长为( )
的实轴长为( )
A. | B. | C. | D. |
已知实数 ,
, ,
, 构成一个等比数列,则圆锥曲线
构成一个等比数列,则圆锥曲线 的离心率为( )
的离心率为( )
A. | B. | C. | D.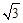 |
椭圆 的左焦点为F,右顶点为A,以FA为直径的圆经过椭圆的上顶点,则椭圆的离心率为( )
的左焦点为F,右顶点为A,以FA为直径的圆经过椭圆的上顶点,则椭圆的离心率为( )
A.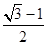 | B. | C. | D. |
已知中心在原点的椭圆C的右焦点为 ,离心率等于
,离心率等于 ,则C的方程是( )
,则C的方程是( )
A. | B. | C. | D. |




 -
- =1(a>0,b>0)的左顶点,且此双曲线的一条渐
=1(a>0,b>0)的左顶点,且此双曲线的一条渐
