题目内容
(本题满分15分)已知椭圆的两焦点为F1(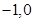 ),F2(1,0),直线x = 4是椭圆的一条准线.
),F2(1,0),直线x = 4是椭圆的一条准线.
(1)求椭圆方程;
(2)设点P在椭圆上,且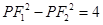 ,求cos∠F1PF2的值;
,求cos∠F1PF2的值;
(3)设P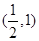 是椭圆内一点,在椭圆上求一点Q,使得
是椭圆内一点,在椭圆上求一点Q,使得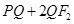 最小.
最小.
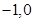 ),F2(1,0),直线x = 4是椭圆的一条准线.
),F2(1,0),直线x = 4是椭圆的一条准线.(1)求椭圆方程;
(2)设点P在椭圆上,且
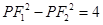 ,求cos∠F1PF2的值;
,求cos∠F1PF2的值;(3)设P
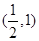 是椭圆内一点,在椭圆上求一点Q,使得
是椭圆内一点,在椭圆上求一点Q,使得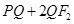 最小.
最小.(1) ;(2)
;(2) ; (3)
; (3)
 ;(2)
;(2) ; (3)
; (3)
略

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
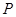 是椭圆
是椭圆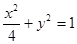 与双曲线
与双曲线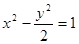 的一个交点,
的一个交点,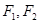 是椭圆的左右焦点,则
是椭圆的左右焦点,则 .
.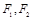 是椭圆
是椭圆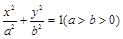 的两个焦点, 若存在点P为椭圆上一点, 使得
的两个焦点, 若存在点P为椭圆上一点, 使得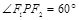 , 则椭圆离心率
, 则椭圆离心率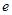 的取值范围是
的取值范围是



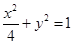 的焦点为
的焦点为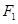 、
、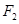 ,在长轴
,在长轴 上任取一点
上任取一点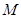 ,过
,过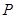 ,则使得
,则使得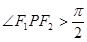 的
的




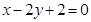 经过椭圆
经过椭圆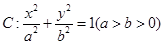 的左顶点
的左顶点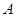 和上顶点
和上顶点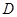 ,椭圆
,椭圆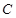 的右顶点为
的右顶点为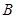 ,点
,点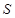 是椭圆
是椭圆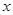 轴上方的动点,直线
轴上方的动点,直线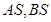 与直线
与直线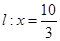 分别交于
分别交于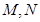 两点.
两点.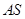 与直线
与直线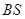 斜率
斜率 的乘积为定值;
的乘积为定值;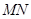 的长度的最小值.
的长度的最小值.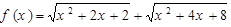 的最小值为( )
的最小值为( )



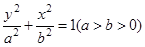 的上焦点是
的上焦点是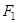 ,过点P(3,4)和
,过点P(3,4)和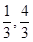 ).
).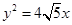 的焦点,离心率是
的焦点,离心率是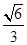
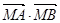 为常数?若存在,求出点M的坐标;若不存在,请说明理由。
为常数?若存在,求出点M的坐标;若不存在,请说明理由。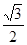 ,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为 __
,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为 __