题目内容
(本题满分14分)已知数列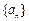 、
、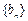 满足
满足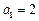 ,
,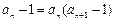 ,
,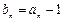 。
。
(Ⅰ)求数列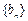 的通项公式;
的通项公式;
(Ⅱ)若数列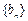 的前
的前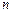 项和为
项和为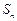 ,设
,设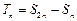 ,求证:
,求证: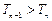 。
。
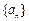 、
、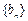 满足
满足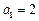 ,
,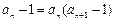 ,
,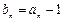 。
。(Ⅰ)求数列
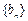 的通项公式;
的通项公式;(Ⅱ)若数列
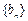 的前
的前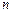 项和为
项和为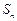 ,设
,设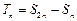 ,求证:
,求证: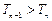 。
。解:(1)由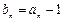 得
得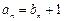 代入
代入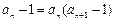 ,
,
得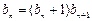 ,整理得
,整理得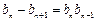 。
。
∵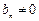 ,否则
,否则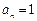 ,与
,与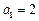 矛盾。
矛盾。
从而得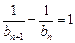 ,
,
∵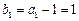 ∴数列
∴数列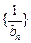 是首项为1,公差为1的等差数列。
是首项为1,公差为1的等差数列。
∴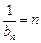 ,即
,即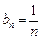 .----------------------------------------
.---------------------------------------- ----------------------7分
----------------------7分
(2)∵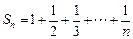 ,
,
∴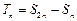 =
=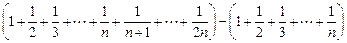
=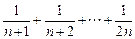 。
。
证法1:∵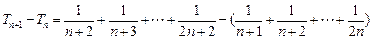
=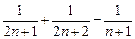
=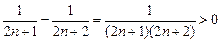
∴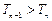 .--------------------------------------------------------------14分
.--------------------------------------------------------------14分
证法2:∵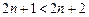 ,∴
,∴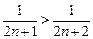 ,
,
∴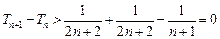 。
。
∴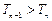 .---------------------------------------------------------------14分
.---------------------------------------------------------------14分
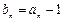 得
得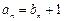 代入
代入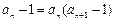 ,
,得
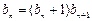 ,整理得
,整理得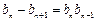 。
。∵
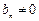 ,否则
,否则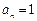 ,与
,与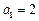 矛盾。
矛盾。从而得
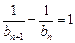 ,
,∵
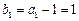 ∴数列
∴数列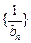 是首项为1,公差为1的等差数列。
是首项为1,公差为1的等差数列。∴
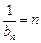 ,即
,即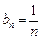 .----------------------------------------
.---------------------------------------- ----------------------7分
----------------------7分(2)∵
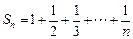 ,
,∴
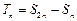 =
=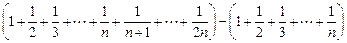
=
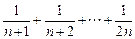 。
。证法1:∵
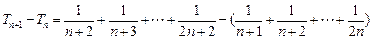
=
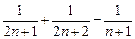
=
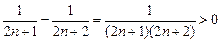
∴
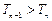 .--------------------------------------------------------------14分
.--------------------------------------------------------------14分证法2:∵
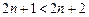 ,∴
,∴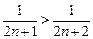 ,
,∴
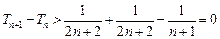 。
。∴
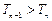 .---------------------------------------------------------------14分
.---------------------------------------------------------------14分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
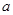 、
、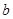 的等差中项是5,则
的等差中项是5,则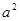 、
、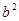 的等比中项的最大值为
的等比中项的最大值为 13分)设等差数列
13分)设等差数列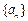 满足
满足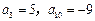 .
. 数列
数列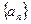 的第10项为23,第25项为
的第10项为23,第25项为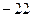 ,
, 数列
数列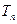 .
.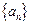 中,
中,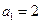 ,
,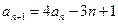 ,
,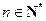 .
.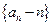 是等比数列;
是等比数列;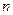 项和
项和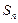 ;
; 3)证明不等式
3)证明不等式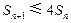 ,对任意
,对任意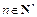 皆成立.
皆成立. 已知数列
已知数列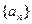 ,其前n项和
,其前n项和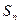 ,满足
,满足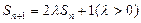 ,且
,且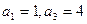
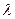 的值;
的值;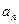 ;
;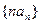 的前
的前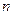 项和为
项和为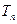 ,试比较
,试比较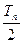 与
与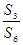 =
= ,则
,则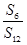 =( )
=( )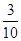
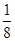
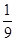
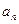 }的前
}的前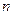 项和为
项和为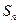 ,且点
,且点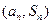 在函数
在函数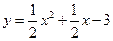 的图象上,
的图象上,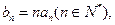 求证:
求证: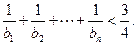
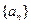 的前
的前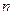 项和
项和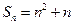 ,则
,则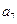 的值为( )
的值为( )