题目内容
(本小题满分12分)
在数列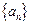 中,
中,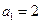 ,
,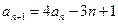 ,
,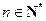 .
.
(1)证明数列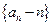 是等比数列;
是等比数列;
(2)求数列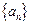 的前
的前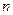 项和
项和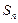 ;
;
( 3)证明不等式
3)证明不等式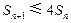 ,对任意
,对任意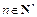 皆成立.
皆成立.
在数列
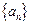 中,
中,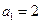 ,
,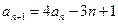 ,
,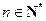 .
.(1)证明数列
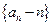 是等比数列;
是等比数列;(2)求数列
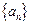 的前
的前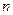 项和
项和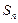 ;
;(
 3)证明不等式
3)证明不等式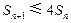 ,对任意
,对任意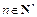 皆成立.
皆成立.(1)证明:由题设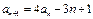 ,得
,得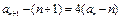 ,
,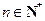 .
.
又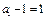 ,所以数列
,所以数列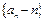 是首项为
是首项为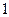 ,且公比为
,且公比为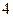 的等比数列.…………………4分
的等比数列.…………………4分
(2)解:由(1)可知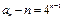 ,于是数列
,于是数列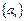 的通项公式为
的通项公式为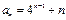 .
.
所以数列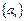 的前
的前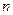 项和
项和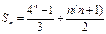 .…………………8分
.…………………8分
(3)证明:对任意的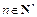 ,
,
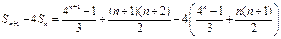
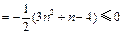 .
.
所以, 不等式
不等式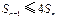 ,对任意
,对任意 皆成立.…………………12分
皆成立.…………………12分
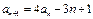 ,得
,得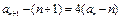 ,
,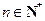 .
.又
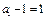 ,所以数列
,所以数列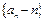 是首项为
是首项为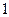 ,且公比为
,且公比为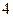 的等比数列.…………………4分
的等比数列.…………………4分(2)解:由(1)可知
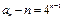 ,于是数列
,于是数列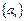 的通项公式为
的通项公式为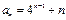 .
.所以数列
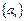 的前
的前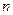 项和
项和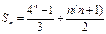 .…………………8分
.…………………8分(3)证明:对任意的
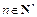 ,
,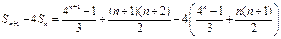
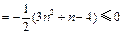 .
.所以,
 不等式
不等式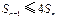 ,对任意
,对任意 皆成立.…………………12分
皆成立.…………………12分略

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
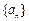 、
、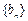 满足
满足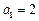 ,
,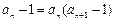 ,
,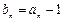 。
。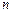 项和为
项和为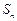 ,设
,设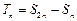 ,求证:
,求证: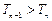 。
。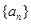 的首项
的首项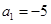 ,它的前11项的平均值为5,若从中抽去一项,余
,它的前11项的平均值为5,若从中抽去一项,余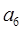
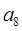
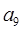
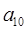
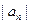 为等差数列,且
为等差数列,且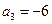 ,
,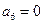 。
。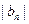 满足
满足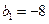 ,
,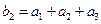 ,求
,求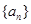 前
前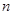 项和为
项和为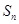 ,若
,若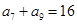 ,
,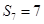 ,则
,则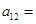 ( )
( )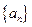 的前
的前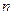 项和为
项和为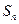 ,若
,若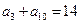 ,则
,则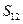 等于_____________.
等于_____________.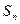 为等差数列
为等差数列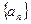 的前
的前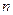 项和,
项和,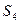 =5,
=5,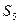 =4,则
=4,则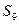 = ;
= ;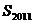 等于____________。
等于____________。