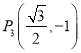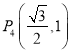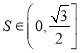题目内容
【题目】已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2![]() ,PC
,PC![]() ,则三棱锥P﹣ABC外接球的表面积为______.
,则三棱锥P﹣ABC外接球的表面积为______.
【答案】![]()
【解析】
由O为△ABC外接圆的圆心,且平面PBC⊥平面ABC,过O作面ABC的垂线l,则垂线l一定在面PBC内,可得球心O1一定在面PBC内,即球心O1也是△PBC外接圆的圆心,
在△PBC中,由余弦定理、正弦定理可得R.
因为O为△ABC外接圆的圆心,且平面PBC⊥平面ABC,过O作面ABC的垂线l,则垂线l一定在面PBC内,
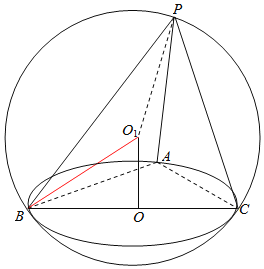
根据球的性质,球心一定在垂线l上,
∵球心O1一定在面PBC内,即球心O1也是△PBC外接圆的圆心,
在△PBC中,由余弦定理得cosB![]() ,sinB
,sinB![]() ,
,
由正弦定理得:![]() ,解得R
,解得R![]() ,
,
∴三棱锥P﹣ABC外接球的表面积为s=4πR2=10π,
故答案为:10π.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目