题目内容
3.已知数列{an}的前n项和为Sn,首项为b,若存在非零常数a,使得(1-a)Sn=b-an+1对一切n∈N*都成立.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)问是否存在一组非零常数a,b,使得{Sn}成等比数列?若存在,求出常数a,b的值,若不存在,请说明理由.
分析 (Ⅰ)由n=1推导出a2=ab=aa1,当n≥2时,由迭代法推导出an+2=a•an+1,由此能求出数列{an}的通项公式.
(Ⅱ)当a=1时,Sn=na1=nb,不合题意,当a≠1时,推导出a=0,与题设矛盾,由此得到不存在非零常数a,b,使得{Sn}成等比数列.
解答 解:(Ⅰ)∵数列{an}的前n项和为Sn,首项为b,
存在非零常数a,使得(1-a)Sn=b-an+1对一切n∈N*都成立,
由题意得当n=1时,(1-a)b=b-a2,∴a2=ab=aa1,
当n≥2时,(1-a)Sn=b-an+1,(1-a)Sn+1=b-an+1,
两式作差,得:an+2=a•an+1,n≥2,
∴{an}是首项为b,公比为a的等比数列,
∴${a}_{n}=b•{a}^{n-1}$.
(Ⅱ)当a=1时,Sn=na1=nb,不合题意,
当a≠1时,${S}_{n}=\frac{b(1-{a}^{n})}{1-a}$,
若$\frac{{S}_{2}}{{S}_{1}}=\frac{{S}_{3}}{{S}_{2}}$,即$\frac{1-{a}^{2}}{1-a}=\frac{1-{a}^{3}}{1-{a}^{2}}$,
化简,得a=0,与题设矛盾,
故不存在非零常数a,b,使得{Sn}成等比数列.
点评 本题考查数列的通项公式的求法,考查使得数列成等比数列的非零常数是否存在的判断与求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.函数 f( x)=10x 3-80的零点为( )
| A. | (2,0) | B. | (0,2) | C. | 2 | D. | 0 |
14.已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)=-x,那么在区间[-1,3]上,关于x的方程f(x)=kx+k-1(其中k为不等于1的实数)有四个不同的实数根,则k的取值范围是( )
| A. | ( ) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{4}$) | D. | (0,$\frac{1}{3}$) |
18.点集{(x,y)|(|x|-1)2+y2=4}表示的图形是一条封闭的曲线,这条封闭曲线所围成的区域面积是( )
| A. | $\frac{16π}{3}+2\sqrt{3}$ | B. | $\frac{16π}{3}+4\sqrt{3}$ | C. | $\frac{24π}{3}+2\sqrt{3}$ | D. | $\frac{24π}{3}+4\sqrt{3}$ |
 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=$\frac{\sqrt{2}}{2}A{A}_{1}$,E是棱A1A的中点,F为棱CC1上的一动点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=$\frac{\sqrt{2}}{2}A{A}_{1}$,E是棱A1A的中点,F为棱CC1上的一动点.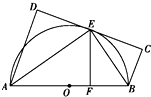 如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.
如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.