题目内容
6.已知F1,F2分别是中心在坐标原点,对称轴为做标轴的双曲线C的左、右焦点,过F2的直线l与双曲线的右支交于A,B两点,I1,I2分别为△AF1F2,△BF1F2的内心,若双曲线C的离心率为2,|I1I2|=$\frac{9}{2}$,直线l的倾斜角的正弦值为$\frac{8}{9}$,则双曲线C的方程为( )| A. | x${\;}^{2}+\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{16}-\frac{{y}^{2}}{48}$=1 | C. | $\frac{{x}^{2}}{2}-\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
分析 充分利用平面几何图形的性质解题.因从同一点出发的切线长相等,得|AM|=|AN|,|F1M|=|F1E|,|F2N|=|F2E|,再结合双曲线的定义得|F1E|-|F2E|=2a,从而即可求得△AF1F2的内心的横坐标a,即有I1I2⊥x轴,在△CF2I2中,运用解直角三角形知识,可得,|I1I2|=(c-a)[tan$\frac{θ}{2}$+tan(90°-$\frac{θ}{2}$)]=(c-a)•$\frac{1+ta{n}^{2}\frac{θ}{2}}{tan\frac{θ}{2}}$
=$\frac{2}{sinθ}$•(c-a)=$\frac{2}{\frac{8}{9}}$•(c-a)=$\frac{9}{2}$,结合双曲线C的离心率为2,求出a,b,c,即可求出双曲线C的方程.
解答 解:记边AF1、AF2、F1F2上的切点分别为M、N、E,
易见I1、E横坐标相等,则|AM|=|AN|,|F1M|=|F1E|,|F2N|=|F2E|,
由|AF1|-|AF2|=2a,
即|AM|+|MF1|-(|AN|+|NF2|)=2a,得|MF1|-|NF2|=2a,
即|F1E|-|F2E|=2a,记I1的横坐标为x0,则E(x0,0),
于是x0+c-(c-x0)=2a,得x0=a,
同样内心I2的横坐标也为a,则有I1I2⊥x轴,
由直线的倾斜角θ的正弦为$\frac{8}{9}$,则∠OF2I2=$\frac{θ}{2}$,∠I1F2O=90°-$\frac{θ}{2}$,
在△I1F2D中,|I1I2|=(c-a)[tan$\frac{θ}{2}$+tan(90°-$\frac{θ}{2}$)]=(c-a)•$\frac{1+ta{n}^{2}\frac{θ}{2}}{tan\frac{θ}{2}}$
=$\frac{2}{sinθ}$•(c-a)=$\frac{2}{\frac{8}{9}}$•(c-a)=$\frac{9}{2}$,
因为双曲线C的离心率为2,所以c=2a,
所以a=2,c=4,b=2$\sqrt{3}$,
故选:D.
点评 本题考查双曲线的定义、方程和性质,考查三角形的内心的概念,考查三角函数的化简和求值,属于中档题.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 |
| 平均气温x(°C) | 29 | 26 | 24 | 22 | 20 |
| 销量y(件) | 11 | 8 | 7 | 5 | 3 |
(1)求选取的2组数据恰好是相邻2天数据的概率;
(2)若选取的是10月1日至2日的两组数据,请根据10月3日至10月5日的数据,求出y关于x的线性回归方程$\hat y=bx+a$;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2件,则认为得到的线性回归方程是可靠的,试问(2)中所得到的线性回归方程是否可靠?

| A. | 7 | B. | 15 | C. | 29 | D. | 31 |
| A. | ( ) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{4}$) | D. | (0,$\frac{1}{3}$) |
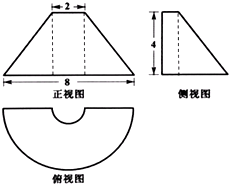 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )| A. | 12+$\frac{47π}{2}$ | B. | 12+23π | C. | 12+24π | D. | 12+$\frac{45}{2}$π |
| A. | $\frac{16π}{3}+2\sqrt{3}$ | B. | $\frac{16π}{3}+4\sqrt{3}$ | C. | $\frac{24π}{3}+2\sqrt{3}$ | D. | $\frac{24π}{3}+4\sqrt{3}$ |
 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=$\frac{\sqrt{2}}{2}A{A}_{1}$,E是棱A1A的中点,F为棱CC1上的一动点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=$\frac{\sqrt{2}}{2}A{A}_{1}$,E是棱A1A的中点,F为棱CC1上的一动点.