题目内容
对于函数y=f(x),如果存在区间[m,n],同时满足下列条件:①f(x)在[m,n]是单调的;②当定义域是[m,n]时,f(x)的值域是[2m,2n],则称[m,n]是该函数的“倍值区间”.若函数f(x)=
+a存在“倍值区间”,则a的取值范围是( )
| x+1 |
A、(-
| ||
B、[-
| ||
C、(-
| ||
D、(-
|
考点:函数的值域
专题:函数的性质及应用
分析:易得函数在区间[m,n]是单调递增的,由f(m)=2m,f(n)=2n,可得故m、n是方程
+a=2x的两个实数根,由此构造函数,分析出满足条件的a的取值范围.
| x+1 |
解答:解:∵函数f(x)=
+a为单调递增函数,
若函数f(x)=
+a存在“倍值区间”,
则f(m)=2m,且f(n)=2n,
故m、n是方程
+a=2x的两个实数根,
即a=2x-
在[-1,+∞)上有两个不等的实根,
令y=2x-
,则y′=2-
,
令y′=2-
=0,则x=-
,
当x∈[-1,-
)时,y′<0,当x∈(-
,+∞)时,y′>0,
故当x=-
时,y=2x-
取最小值-
,
又∵当x=-1时,y=2x-
=-2,
2x-
=+∞,
故若a=2x-
在[-1,+∞)上有两个不等的实根,
a∈(-
,-2],
故选:D
| x+1 |
若函数f(x)=
| x+1 |
则f(m)=2m,且f(n)=2n,
故m、n是方程
| x+1 |
即a=2x-
| x+1 |
令y=2x-
| x+1 |
| 1 | ||
2
|
令y′=2-
| 1 | ||
2
|
| 15 |
| 16 |
当x∈[-1,-
| 15 |
| 16 |
| 15 |
| 16 |
故当x=-
| 15 |
| 16 |
| x+1 |
| 7 |
| 8 |
又∵当x=-1时,y=2x-
| x+1 |
| lim |
| x→∞ |
| x+1 |
故若a=2x-
| x+1 |
a∈(-
| 17 |
| 8 |
故选:D
点评:本题考查的知识点是函数的单调性,恒成立问题,利用导数求函数的最值,是函数与导数的综合应用,难度较大.

练习册系列答案
相关题目
已知全集U=R,集合A={x|2x>1},B={x|-4<x<1},则A∩B等于( )
| A、(0,1) | B、(1,+∞) | C、(-4,1) | D、(-∞,-4) |
设全集U={1,2,3,4,5},集合A={2,3,4},集合B={3,5},则B∩∁UA=( )
| A、{5} | B、{1,2,3,4,5} | C、{1,3,5} | D、∅ |
设集合A={x||x-1|≤2},B={x|x2-3x-4≤0},则∁R(A∩B)=( )
| A、(-∞,-1)∪(1,+∞) | B、(-∞,3)∪(4,+∞) | C、(-∞,2)∪(2,+∞) | D、(-∞,-1)∪(3,+∞) |
已知全集U=R,集合A={x|
>0},B={x|y=
},则A∩B=( )
| x-1 |
| 3-x |
| 4-2x |
| A、(1,2) |
| B、(2,3) |
| C、[2,3) |
| D、(1,2] |
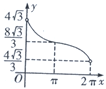
下列四个图中,哪个可能是函数y=
的图象( )
| 10ln|x+1| |
| x+1 |
A、 |
B、 |
C、 |
D、 |
已知函数f(x)=-2x3-x,若x1,x2,x3∈R,且x1+x2>0,x2+x3>0,x3+x1>0,则f(x1)+f(x2)+f(x3)的值( )
| A、大于零 | B、小于零 | C、等于零 | D、大于零或小于零 |
设函数f(x)=
,则满足f(x)≤3的x的取值范围是( )
|
| A、[0,+∞) |
| B、[-1,3] |
| C、[0,3] |
| D、[1,+∞) |
 如图,半径为1的圆O与等边三角形ABC夹在两平行直线l1,l2之间,l∥l1与圆相交于F,G两点.与三角形ABC两边交于E,D两点,设弧
如图,半径为1的圆O与等边三角形ABC夹在两平行直线l1,l2之间,l∥l1与圆相交于F,G两点.与三角形ABC两边交于E,D两点,设弧