题目内容
【题目】已知x,y∈R,且 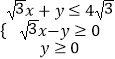 ,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )
,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]() ﹣
﹣ ![]()
C.![]()
D.![]() +
+ ![]()
【答案】A
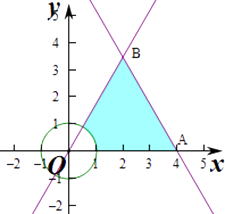
【解析】解:作出不等式组对应的平面区域如图:对应的区域为三角形OAB,
若存在θ∈R,使得xcosθ+ysinθ+1=0成立,
则 ![]() (
( ![]() cosθ+
cosθ+ ![]() sinθ)=﹣1,
sinθ)=﹣1,
令sinα= ![]() ,则cosθ=
,则cosθ= ![]() ,
,
则方程等价为 ![]() sin(α+θ)=﹣1,
sin(α+θ)=﹣1,
即sin(α+θ)=﹣ ![]() ,
,
∵存在θ∈R,使得xcosθ+ysinθ+1=0成立,
∴|﹣ ![]() |≤1,即x2+y2≥1,
|≤1,即x2+y2≥1,
则对应的区域为单位圆的外部,
由 ![]() ,解得
,解得 ![]() ,即B(2,2
,即B(2,2 ![]() ),
),
A(4,0),则三角形OAB的面积S= ![]() ×
× ![]() =4
=4 ![]() ,
,
直线y= ![]() x的倾斜角为
x的倾斜角为 ![]() ,
,
则∠AOB= ![]() ,即扇形的面积为
,即扇形的面积为 ![]() ,
,
则P(x,y)构成的区域面积为S=4 ![]() ﹣
﹣ ![]() ,
,
故选:A

练习册系列答案
相关题目


