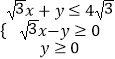题目内容
【题目】已知双曲线![]() 的离心率为2,
的离心率为2,![]() 分别是双曲线的左、右焦点,点
分别是双曲线的左、右焦点,点![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的动点,当
上的动点,当![]() 取得最小值和最大值时,
取得最小值和最大值时,![]() 的面积分别为
的面积分别为![]() ,则
,则![]() ____________.
____________.
【答案】![]()
【解析】
利用双曲线的离心率推出b=![]() a,线段MN所在直线的方程为y=
a,线段MN所在直线的方程为y=![]() (x+a),点P在线段MN上,可设P(m,
(x+a),点P在线段MN上,可设P(m,![]() (m+a)), 其中m∈[-a,0],由F1(-c,0),F2(c,0),通过斜率的数量积求出
(m+a)), 其中m∈[-a,0],由F1(-c,0),F2(c,0),通过斜率的数量积求出![]() 的最值,然后求解结果.
的最值,然后求解结果.
由已知e=![]() =2得c=2a,b=
=2得c=2a,b=![]() a,故线段MN所在直线的方程为y=
a,故线段MN所在直线的方程为y=![]() (x+a),又点P在线段MN上,可设P(m,
(x+a),又点P在线段MN上,可设P(m,![]() (m+a)),其中m∈[-a,0],由F1(-c,0),F2(c,0),得
(m+a)),其中m∈[-a,0],由F1(-c,0),F2(c,0),得![]() =(2am,
=(2am,![]() (m+a)),
(m+a)),![]() (2am,
(2am,![]() (m+a))),则
(m+a))),则![]() 4m2+6am
4m2+6am![]() ,由m∈[-a,0],可知当m=-
,由m∈[-a,0],可知当m=-![]() a时,
a时,![]() 取得最小值,此时S1=
取得最小值,此时S1=![]() ×2c×
×2c×![]() (-
(-![]() a+a)=
a+a)=![]() ac,当m=0时,
ac,当m=0时,![]() 取得最大值,此时S2=
取得最大值,此时S2=![]() ×2c×
×2c×![]() a=
a=![]()
ac,所以![]()
![]() .
.
故答案为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目