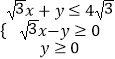题目内容
【题目】如图，在三棱锥P﹣ABC中，AC=BC=2，∠ACB=90°，侧面PAB为等边三角形，侧棱 
． 
（Ⅰ）求证：PC⊥AB；
（Ⅱ）求证：平面PAB⊥平面ABC；
（Ⅲ）求二面角B﹣AP﹣C的余弦值．
【答案】解：（Ⅰ）设AB中点为D，连接PD，CD，
因为AP=BP，所以PD⊥AB．
又AC=BC，所以CD⊥AB．
因为PD∩CD=D，所以AB⊥平面PCD．
因为PC平面PCD，所以PC⊥AB．
（Ⅱ）由已知∠ACB=90°，AC=BC=2，
所以 
， 
．
又△PAB为正三角形，且PD⊥AB，所以 
．
因为 
，所以PC2=CD2+PD2．
所以∠CDP=90°．
由（Ⅰ）知∠CDP是二面角P﹣AB﹣C的平面角．
所以平面PAB⊥平面ABC．
（Ⅲ）方法1：由（Ⅱ）知CD⊥平面PAB．
过D作DE⊥PA于E，连接CE，则CE⊥PA．
所以∠DEC是二面角B﹣AP﹣C的平面角．
在Rt△CDE中，易求得 
．
因为 
，所以 
．
所以 
．
即二面角B﹣AP﹣C的余弦值为 
．
方法2：由（Ⅰ）（Ⅱ）知DC，DB，DP两两垂直．
以D为原点建立如图所示的空间直角坐标系．
易知D（0，0，0）， 
， 
， 
．所以 
， 
．
设平面PAC的法向量为n=（x，y，z），
则 
即 
令x=1，则y=﹣1， 
．
所以平面PAC的一个法向量为 
．
易知平面PAB的一个法向量为 
．
所以 
．
由图可知，二面角B﹣AP﹣C为锐角．
所以二面角B﹣AP﹣C的余弦值为 ．
【解析】（Ⅰ）由题意，证明PC⊥AB可通过证明AB⊥平面PCD，用线面垂直证线线垂直；（II）要证明两个平面垂直，可以证明两个平面所成的二面角是直角，根据三边长满足勾股定理得到直角，得到结论．（III）方法一：过D作DE⊥PA于E，接CE，则CE⊥PA．所以∠DEC是二面角B﹣AP﹣C的平面角，在三角形中求角即可；方法二：（空间向量法）以D为原点建立如图所示的空间直角坐标系，给出各点的坐标，建立方程求出两个平面的法向量，用公式求出二面角的余弦值，
【考点精析】掌握平面与平面垂直的判定是解答本题的根本，需要知道一个平面过另一个平面的垂线，则这两个平面垂直．
