Question

20．（1）已知不等式ax²-3x+6＞4的解集为{x|x＜1或x＞b}，求出a，b并解不等式（x-c）（ax-b）＞0
（2）已知线段AB长为$\sqrt{7}$，其正视图长为$\sqrt{6}$，侧视图长为a，俯视图长为b，求a+b的最大值．

Answer 1

分析 （1）运用二次方程根与系数的关系式，即可求出a，b，）将原不等式转化为（x-c）（x-2）＞0，对c讨论，分c=2，c＞2，c＜2三种情况，写出解集即可；
（2）由棱和它在三视图中的投影扩展为长方体，三视图中的三个投影，是三个面对角线，设出三度，利用勾股定理，基本不等式求出最大值．

解答 解：（1）由已知1，b是方程ax²-3x+2=0的两根，
∴1+b=$\frac{3}{a}$，b=$\frac{2}{a}$，
解得a=1，b=2，
∴不等式（x-c）（ax-b）＞0化为（x-c）（x-2）＞0
当c＜2时解集为（-∞，c）∪（2，+∞），
当c＞2时解集为（-∞，2）∪（c，+∞），
当c=2时解集为（-∞，2）∪（2，+∞），
（2）如图设以AB为对角线的长方体长为x，宽为y，高为z，则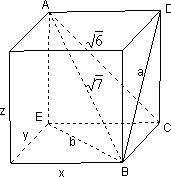$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}+{z}^{2}=7}\\{{x}^{2}+{z}^{2}=6}\\{{y}^{2}+{z}^{2}={a}^{2}}\\{{x}^{2}+{y}^{2}={b}^{2}}\end{array}\right.$，
∴a²+b²=8，
∴a+b≤2$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$=4，当且仅当a=b=2时取等号，
∴a+b的最大值为4．

点评 本题主要考查含参一元二次不等式的解法，考查分类讨论的思想方法，还考查三视图，几何体的结构特征，考查空间想象能力，基本不等式的应用，是中档题．