题目内容
【题目】如图,在三棱锥S﹣ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D,E分别是AC,BC的中点,F在SE上,且SF=2FE. 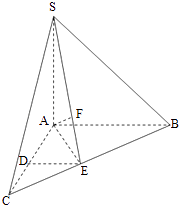
(1)求证:AF⊥平面SBC;
(2)在线段上DE上是否存在点G,使二面角G﹣AF﹣E的大小为30°?若存在,求出DG的长;若不存在,请说明理由.
【答案】
(1)证明:由AC=AB=SA=2,AC⊥AB,E是BC的中点,得 ![]() .
.
因为SA⊥底面ABC,所以SA⊥AE.
在Rt△SAE中, ![]() ,所以
,所以 ![]() .
.
因此AE2=EFSE,又因为∠AEF=∠AES,
所以△EFA∽△EAS,
则∠AFE=∠SAE=90°,即AF⊥SE.
因为SA⊥底面ABC,所以SA⊥BC,又BC⊥AE,
所以BC⊥底面SAE,则BC⊥AF.
又SE∩BC=E,所以AF⊥平面SBC
(2)解:结论:在线段上DE上存在点G使二面角G﹣AF﹣E的大小为30°,此时DG= ![]() .
.
理由如下:
假设满足条件的点G存在,并设DG=t.
过点G作GM⊥AE交AE于点M,
又由SA⊥GM,AE∩SA=A,得GM⊥平面SAE.
作MN⊥AF交AF于点N,连结NG,则AF⊥NG.
于是∠GNM为二面角G﹣AF﹣E的平面角,
即∠GNM=30°,由此可得 ![]() .
.
由MN∥EF,得 ![]() ,
,
于是有 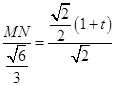 ,
, ![]() .
.
在Rt△GMN中,MG=MNtan30°,
即 ![]() ,解得
,解得 ![]() .
.
于是满足条件的点G存在,且 ![]() .
.
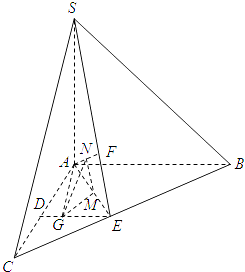
【解析】(1)通过证明AF与平面SBC内的两条相交直线垂直即可;(2)抓住两点找到问题的求解方向:一是点G的预设位置,二是二面角G﹣AF﹣E的位置,计算即可.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

【题目】某医疗科研项目对5只实验小白鼠体内的A、B两项指标数据进行收集和分析,得到的数据如下表:
指标 | 1号小白鼠 | 2号小白鼠 | 3号小白鼠 | 4号小白鼠 | 5号小白鼠 |
A | 5 | 7 | 6 | 9 | 8 |
B | 2 | 2 | 3 | 4 | 4 |
(1)若通过数据分析,得知A项指标数据与B项指标数据具有线性相关关系,试根据上表,求B项指标数据y关于A项指标数据x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)现要从这5只小白鼠中随机抽取3只,求其中至少有一只B项指标数据高于3的概率. 参考公式: ![]() =
= 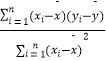 =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.