Question

【题目】在正方形中，，是中点，将和分别沿若、翻折，使得、两点重合，则所形成的立体图形的外接球的表面积是（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

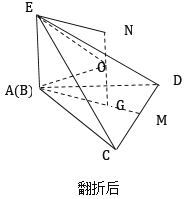
根据题意，作出翻折后的几何体，取中点，记外接圆圆心为，过点作平面，由题中条件得到，记几何体外接球球心为，连接，得到，再由题中数据，即可求出外接球半径，从而可得出球的表面积.

由题意，作出翻折后的几何体如图所示：

取中点，记外接圆圆心为，

因为在正方形中，，所以翻折后，为等边三角形，

则外接圆圆心即是重心，

所以三点共线，且；

过点作平面，记所求几何体外接球球心为，外接球半径为，

则球心在直线上，连接，则

又，，所以翻折后，，，

所以平面，因此，

又，所以是等腰三角形，

易得，

所以，

故所求外接球表面积为.

故选B