Question

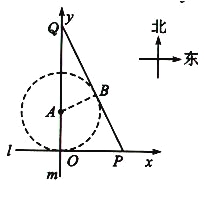
【题目】如图，某市有一条东西走向的公路l，现欲经过公路l上的O处铺设一条南北走向的公路m，在施工过程中发现O处的正北方向1百米的A处有一汉代古迹，为了保护古迹，该市委决定以A为圆心，1百米为半径设立一个圆形保护区，为了连通公路l，m，欲再新建一条公路PQ，点P，Q分别在公路l，m上（点P，Q分别在点O的正东、正北方向），且要求PQ与圆A相切.

（1）当点P距O处2百米时，求OQ的长；

（2）当公路PQ的长最短时，求OQ的长.

Answer 1

【答案】（1）（2）

【解析】

试题分析：（1）根据题意，建立直角坐标系，然后利用直线与圆的相切列出关于关于q的方程解之即可；

（2）利用截距式方程给出直线的方程，然后利用直线与圆相切找到两个待定系数间的关系，再利用勾股定理将PQ表示成关于q的函数，利用函数的单调性求其最值即可

试题解析：如图，以O为原点、直线l，m分别为x，y轴建立平面直角坐标系.

设P（p, 0），Q（0, q）且PQ与圆A相切于点B，连结AB，以1百米为单位长度，则圆A的方程为

（1）由题意可设直线PQ的方程为，

即

因为PQ与圆A相切，

所以，解得，

故当点P与O处2百米时，OQ的长为百米.

（2）设直线PQ的方程为，

即.

因为PQ与圆A相切，

所以，化简得

在Pt△POQ中，.

令

则

当时，，即f(q)在（上单调递减；

当时，，即f(q)在上单调递增.

所以f(q)在时取得最小值，

故当公路PQ的长最短时，OQ的长为百米.

答：（1）当点P距O处2百米时，OQ的长为百米；（2）当公路PQ的长最短时，OQ的长为百米.