题目内容
【题目】已知函数![]() ,
,![]() .
.
(I)求函数![]() 的最大值;
的最大值;
(II)当![]() 时,函数
时,函数![]() 有最小值,记
有最小值,记![]() 的最小值为
的最小值为![]() ,求函数
,求函数![]() 的值域.
的值域.
【答案】(I)最大值![]() (II)
(II)![]() .
.
【解析】分析:(I)求出函数的定义域和导数,利用导数的符号变化判定函数的单调性,进而得到函数的最值;(II)求导,利用导数的符号变化和分类讨论思想判定函数![]() 的单调性和最值,即得到
的单调性和最值,即得到![]() 的表达式,再构造函数,利用导数求其最值.
的表达式,再构造函数,利用导数求其最值.
详解:(I)f(x)的定义域为![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
(II)![]() ,由(I)及
,由(I)及![]() 得:
得:
若![]() ,
,![]() ,
,![]() ,g(x)单调递减,
,g(x)单调递减,
当![]() 时,g(x)的最小值
时,g(x)的最小值![]() .
.
②若![]() ,
,![]() ,
,![]() ,
,
所以存![]() ,
,![]() 且
且![]() ,
,
当![]() 时,
时,![]() ,g(x)单调递减;当
,g(x)单调递减;当![]() 时,
时,![]() ,g(x)单调递增,所以g(x)的最小值
,g(x)单调递增,所以g(x)的最小值![]() .
.
令![]() ,
,![]() .
. ![]() ,
,
当![]()
![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递减,此时
单调递减,此时![]() ,即
,即
![]() .
.
由①②可知,h(a)的值域是![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】近年来,人们对食品安全越来越重视,有机蔬菜的需求也越来越大,国家也制定出台了一系列支持有机肥产业发展的优惠政策,鼓励和引导农民增施有机肥,“藏粮于地,藏粮于技”.根据某种植基地对某种有机蔬菜产量与有机肥用量的统计,每个有机蔬菜大棚产量的增加量![]() (百斤)与使用有机肥料
(百斤)与使用有机肥料![]() (千克)之间对应数据如下表:
(千克)之间对应数据如下表:
使用有机肥料 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
产量增加量 | 2.1 | 2.9 | 3.5 | 4.2 | 4.8 | 5.6 | 6.2 | 6.7 |
(1)根据表中的数据,试建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (精确到
(精确到![]() );
);
(2) 若种植基地每天早上7点将采摘的某有机蔬菜以每千克10元的价格销售到某超市,超市以每千克15元的价格卖给顾客.已知该超市每天8点开始营业,22点结束营业,超市规定:如果当天16点前该有机蔬菜没卖完,则以每千克5元的促销价格卖给顾客(根据经验,当天都能全部卖完).该超市统计了100天该有机蔬菜在每天的16点前的销售量(单位:千克),如表:
每天16点前的 销售量(单位:千克) | 100 | 110 | 120 | 130 | 140 | 150 | 160 |
频数 | 10 | 20 | 16 | 16 | 14 | 14 | 10 |
若以100天记录的频率作为每天16点前销售量发生的概率,以该超市当天销售该有机蔬菜利润的期望值为决策依据,说明该超市选择购进该有机蔬菜110千克还是120千克,能使获得的利润更大?
附:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为: 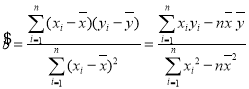 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
【题目】某校在本校任选了一个班级,对全班50名学生进行了作业量的调查,根据调查结果统计后,得到如下的![]() 列联表,已知在这50人中随机抽取2人,这2人都“认为作业量大”的概率为
列联表,已知在这50人中随机抽取2人,这2人都“认为作业量大”的概率为![]() .
.
认为作业量大 | 认为作业量不大 | 合计 | |
男生 | 18 | ||
女生 | 17 | ||
合计 | 50 |
(1)请完成上面的列联表;
(2)根据列联表的数据,能否有![]() 的把握认为“认为作业量大”与“性别”有关?
的把握认为“认为作业量大”与“性别”有关?
附表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
附: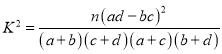 (其中
(其中![]() )
)

