题目内容
已知△ABC的内角A,B,C的对边分别为a,b,c,∠B=
(1)若a=2,b=2
,求c的值;
(2)若tanA=2
,求tanC的值.
| π |
| 3 |
(1)若a=2,b=2
| 3 |
(2)若tanA=2
| 3 |
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)△ABC中,由条件利用余弦定理可得b2=12=4+c2-4c•cos
,由此求得c的值.
(2)由tanA=2
,tanB=tan
=
,再根据tanC=-tan(A+B)=
,计算求得结果.
| π |
| 3 |
(2)由tanA=2
| 3 |
| π |
| 3 |
| 3 |
| tanA+tanB |
| tanAtanB-1 |
解答:
解:(1)△ABC中,∵a=2,b=2
,∠B=
,由余弦定理可得 b2=12=4+c2-4c•cos
=4+c2-2c,
求得c=4,或c=-2(舍去),即c=4.
(2)若tanA=2
,∵tanB=tan
=
,∴tanC=-tan(A+B)=
=
=
.
| 3 |
| π |
| 3 |
| π |
| 3 |
求得c=4,或c=-2(舍去),即c=4.
(2)若tanA=2
| 3 |
| π |
| 3 |
| 3 |
| tanA+tanB |
| tanAtanB-1 |
2
| ||||
2
|
3
| ||
| 5 |
点评:本题主要考查余弦定理、两角和的正切公式,属于基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
tan
π的值为( )
| 16 |
| 3 |
A、-
| ||||
B、
| ||||
C、
|
抛物线y2=2px三点的纵坐标的平方成等差数列,则这三点的横坐标( )
| A、成等差数列 |
| B、成等比数列 |
| C、即成等差数列又成等比数列 |
| D、即不成等差数列又不成等比数列 |
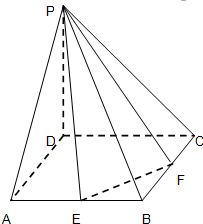 已知正方形ABCD,边长为1,过D作PD⊥平面ABCD,且PD=2,E,F分别是AB和BC的中点.
已知正方形ABCD,边长为1,过D作PD⊥平面ABCD,且PD=2,E,F分别是AB和BC的中点.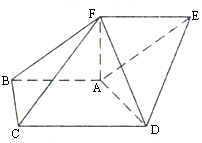 在五面体ABCDEF中,AB∥DC,∠BAD=
在五面体ABCDEF中,AB∥DC,∠BAD=