题目内容
已知f(x)=x2-2|x-a|,当a>O时,若对任意的x∈[O,+∞),不等式f(x-1)≥2f(x)恒成立,求a的值.
考点:函数恒成立问题
专题:函数的性质及应用
分析:先整理f(x-1)≤2f(x)的表达式,有绝对值的放到左边,然后分①0≤x≤a②a<x≤1+a③x>1+a讨论,首先去掉绝对值,然后整理成关于x的一元二次不等式恒成立的问题,利用函数的单调性求出最值,从而求出a的范围,最后求它们的交集.
解答:
解:不等式f(x-1)≥2f(x)化为-(x-1)2+2|x-1-a|≥-2x2+4|x-a|,
即:4|x-a|-2|x-(1+a)|≤x2+2x-1(*)
对任意的x∈[0,+∞)恒成立.
因为a>0.所以分如下情况讨论:
①0≤x≤a时,不等式(*)化为-4(x-a)+2[x-(1+a)]≤x2+2x-1,
即x2+4x+1-2a≥0对任意的x∈[0,a]恒成立,
因为函数g(x)=x2+4x+1-2a在区间[0,a]上单调递增,
则g(0)最小,所以只需g(0)≥0即可,得a≤
,
又a>0所以0<a≤
,
②a<x≤1+a时,不等式(*)化为4(x-a)+2[x-(1+a)]≤x2+2x-1,
即x2-4x+1+6a≥0对任意的x∈(a,1+a]恒成立,
由①,0<a≤
,知:函数h(x)=x2-4x+1+6a在区间(a,1+a]上单调递减,
则只需h(1+a)≥0即可,即a2+4a-2≥0,得a≤-2-
或a≥-2+
.
因为-2+
<
,所以由①得-2+
≤a≤
,
③x>1+a时,不等式(*)化为4(x-a)-2[x-(1+a)]≥x2+2x-1,
即x2+2a-3≥0对任意的x∈(a+1,+∞)恒成立,
因为函数φ(x)=x2+2a-3在区间(a+1,+∞)上单调递增,
则只需φ(a+1)≥0即可,
即a2+4a-2≥0,得或a≤-2-
或a≥-2+
.
由②得-2+
≤a≤
,
综上所述得,a的取值范围是[-2+
,
]
即:4|x-a|-2|x-(1+a)|≤x2+2x-1(*)
对任意的x∈[0,+∞)恒成立.
因为a>0.所以分如下情况讨论:
①0≤x≤a时,不等式(*)化为-4(x-a)+2[x-(1+a)]≤x2+2x-1,
即x2+4x+1-2a≥0对任意的x∈[0,a]恒成立,
因为函数g(x)=x2+4x+1-2a在区间[0,a]上单调递增,
则g(0)最小,所以只需g(0)≥0即可,得a≤
| 1 |
| 2 |
又a>0所以0<a≤
| 1 |
| 2 |
②a<x≤1+a时,不等式(*)化为4(x-a)+2[x-(1+a)]≤x2+2x-1,
即x2-4x+1+6a≥0对任意的x∈(a,1+a]恒成立,
由①,0<a≤
| 1 |
| 2 |
则只需h(1+a)≥0即可,即a2+4a-2≥0,得a≤-2-
| 6 |
| 6 |
因为-2+
| 6 |
| 1 |
| 2 |
| 6 |
| 1 |
| 2 |
③x>1+a时,不等式(*)化为4(x-a)-2[x-(1+a)]≥x2+2x-1,
即x2+2a-3≥0对任意的x∈(a+1,+∞)恒成立,
因为函数φ(x)=x2+2a-3在区间(a+1,+∞)上单调递增,
则只需φ(a+1)≥0即可,
即a2+4a-2≥0,得或a≤-2-
| 6 |
| 6 |
由②得-2+
| 6 |
| 1 |
| 2 |
综上所述得,a的取值范围是[-2+
| 6 |
| 1 |
| 2 |
点评:本题是函数的综合题,考查了函数恒成立的一个常用结论:a>f(x)恒成立,只要a>f(x)的最大值;a<f(x)恒成立,只要a<f(x)的最小值.还重点考查了数学中一个重要数学数学方法--分类讨论.本题属于难题.

练习册系列答案
相关题目
函数f(x)=2sin(2x-
)的图象上的点的横坐标变成原来的4倍(纵坐标不变)再图象上的点向左平移
个单位,向下平移1个单位以后得到的函数的一个对称轴方程为( )
| π |
| 6 |
| π |
| 3 |
A、x=
| ||
B、x=
| ||
| C、x=π | ||
| D、x=2π |
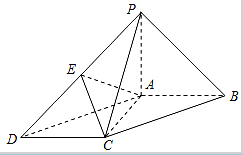 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.