Question

【题目】如图，在平面直角坐标系xOy中，已知R（x0 ， y0）是椭圆C： =1上的一点，从原点O向圆R：（x﹣x0）2+（y﹣y0）2=8作两条切线，分别交椭圆于点P，Q．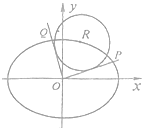
（1）若R点在第一象限，且直线OP，OQ互相垂直，求圆R的方程；
（2）若直线OP，OQ的斜率存在，并记为k1 ， k2 ， 求k1k2的值；
（3）试问OP2+OQ2是否为定值？若是，求出该值；若不是，说明理由．

Answer 1

【答案】
（1）解：由圆R的方程知圆R的半径 ，

因为直线OP，OQ互相垂直，且和圆R相切，

所以 ，即 ①

又点R在椭圆C上，所以 ②

联立①②，解得 ，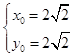

所以，所求圆R的方程为

（2）解：因为直线OP：y=k1x和OQ：y=k2x都与圆R相切，

所以 ， ，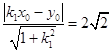

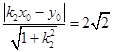两边平方可得k1，k2为（x02﹣8）k2﹣2x0y0k+（y02﹣8）=0的两根，

可得 ，

因为点R（x0，y0）在椭圆C上，

所以 ，即 ，

所以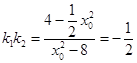

（3）解：方法一①当直线OP，OQ不落在坐标轴上时，

设P（x1，y1），Q（x2，y2），

由（2）知2k1k2+1=0，

所以 ，故 ．

因为P（x1，y1），Q（x2，y2）在椭圆C上，

所以 ，

即 ，

所以 ，

整理得 ，

所以

所以 ．

方法（二）①当直线OP，OQ不落在坐标轴上时，

设P（x1，y1），Q（x2，y2），

联立 ，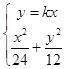

解得 ，

所以 ，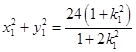

同理，得 ．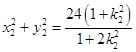

由（2）2k1k2+1=0，得 ，

所以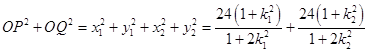

= ，

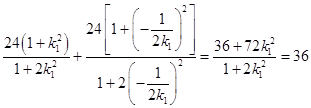②当直线OP，OQ落在坐标轴上时，显然有OP2+OQ2=36．

综上：OP2+OQ2=36．

【解析】（1）求得圆的半径r，由两直线垂直和相切的性质，可得|OR|=4，解方程可得圆心R的坐标，进而得到圆的方程；（2）设出直线OP：y=k1x和OQ：y=k2x，由直线和圆相切的条件：d=r，化简整理，运用韦达定理，由R在椭圆上，即可得到k1k2的值；（3）讨论①当直线OP，OQ不落在坐标轴上时，设P（x1 ， y1），Q（x2 ， y2），运用点满足椭圆方程，由两点的距离公式，化简整理，即可得到定值36；②当直线OP，OQ落在坐标轴上时，显然有OP2+OQ2=36．