题目内容
【题目】已知正方体ABCD﹣A1B1C1D1的棱长为1,给出下列四个命题: ①对角线AC1被平面A1BD和平面B1 CD1三等分;
②正方体的内切球、与各条棱相切的球、外接球的表面积之比为1:2:3;
③以正方体的顶点为顶点的四面体的体积都是 ![]() ;
;
④正方体与以A为球心,1为半径的球在该正方体内部部分的体积之比为6:π
其中正确命题的序号为 . 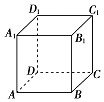
【答案】①②④
【解析】解:∵正方体ABCD﹣A1B1C1D1的棱长为1, 故对角线AC1= ![]() ,
,
棱锥A﹣A1BD的体积为: ![]() ×1×1×1=
×1×1×1= ![]() .
.
平面A1BD的面积为: ![]()
故A到平面A1BD的距离为: ![]() ,
,
故对角线AC1被平面A1BD和平面B1 CD1三等分,
即①正确;
正方体的内切球、与各条棱相切的球、外接球的半径分别为: ![]() ,
, ![]() ,
, ![]() ,
,
故正方体的内切球、与各条棱相切的球、外接球的表面积之比为1:2:3,
故②正确;
以正方体的顶点为顶点的四面体的体积为 ![]() 或
或 ![]() ;
;
故③错误;
以A为球心,1为半径的球在该正方体内部部分的体积为 ![]() =
= ![]() π
π
故正方体与以A为球心,1为半径的球在该正方体内部部分的体积之比为6:π
故④正确;
所以答案是:①②④
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.

练习册系列答案
相关题目