题目内容
椭圆
的离心率
，
.
（1）求椭圆C的方程；
（2）如图，
是椭圆C的顶点，P是椭圆C上除顶点外的任意一点，直线DP交
轴于点N，直线AD交BP于点M。设BP的斜率为
，MN的斜率为
.证明：
为定值。
的离心率，.（1）求椭圆C的方程；
（2）如图，
是椭圆C的顶点，P是椭圆C上除顶点外的任意一点，直线DP交轴于点N，直线AD交BP于点M。设BP的斜率为，MN的斜率为.证明：为定值。（1）
（2）见解析
（2）见解析（1）
，
由（1)知A(-2，0),B(2，0),D(0，1),则直线AD方程为：
；直线BP方程：
，联立得
直线BP和椭圆联立方程组解得P点坐标为
，因为D,N（x,0),P三点共线,所以有：
，由（1)知A(-2，0),B(2，0),D(0，1),则直线AD方程为：
；直线BP方程：，联立得直线BP和椭圆联立方程组解得P点坐标为，因为D,N（x,0),P三点共线,所以有：
练习册系列答案
阳光课堂同步练习系列答案
相关题目
.
为圆O：
的弦AB的中点，则直线AB的斜率
与直线OE的斜率
的乘积
为定值。类比圆的这个性质，写出椭圆
的类似性质，并加以证明；
的切线
，
上任意一点
作
上运动时，是否存在定圆恒与直线MN相切？若存在，求出圆的方程；若不存在，请说明理由.
的离心率为
，点
在椭圆上.
的动直线与椭圆交于M，N两点，连接AN、BM相交于G点，试求点G的横坐标的值.
与椭圆
相交于
两点，点
是线段
上的一点，
且点
上.
的对称点在单位圆
上，求椭圆的方程.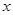
轴的椭圆
的左、右焦点分别为
，直线
过右焦点
，和椭圆交于
两点，且满足
， 
，则椭圆
的标准方程为（ ）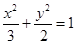
：
（
）过点
，且椭圆
．
在直线
上，过
两点，且
中点，再过
．求直线
是否恒过定点，如果是则求出该定点的坐标，不是请说明理由。
，过点
且离心率为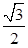
.
的方程；
是椭圆
，连接AM交椭圆于点P，在x轴上是否存在异于A、B的定点Q,使得直线BP和直线MQ垂直.
中，椭圆
的中心为原点，焦点
在
轴上，离心率为
。过
的直线L交C于
两点，且
的周长为16，那么
的中心和左焦点，点P为椭圆上的任意一点，则
的最大值为（ ）