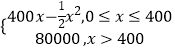题目内容
【题目】已知函数![]() 的两个零点为
的两个零点为![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)求证: ![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析: (1)方法一的思路是:求出函数![]() 的最大值,有两个零点,再最大值一定大于零,求出实数
的最大值,有两个零点,再最大值一定大于零,求出实数![]() 的范围.方法二是转化为两个函数的图象有两个交点; (2)采用综合法和分析法证明不等式.构造函数
的范围.方法二是转化为两个函数的图象有两个交点; (2)采用综合法和分析法证明不等式.构造函数![]() ,利用单调性求出
,利用单调性求出![]() 的范围,构造函数
的范围,构造函数![]() ,证明
,证明![]() 在
在![]() 上为增函数,
上为增函数, ![]() ,化简,得证.
,化简,得证.
试题解析:(1)方法一: ![]() ,
,
①![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增,不可能有两个零点.
上单调递增,不可能有两个零点.
②![]() 时,由
时,由![]() 可解得
可解得![]() ,由
,由![]() 可解得
可解得![]() .
.
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,于是
上单调递增,于是![]() .
.
要使得![]() 在
在![]() 上有两个零点,则
上有两个零点,则![]() ,解得
,解得![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
方法二: ![]() ,可转化为函数
,可转化为函数![]() 与函数
与函数![]() 图象有两个交点.
图象有两个交点.
∵![]() ,∴当
,∴当![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() .即
.即![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴![]() .
.
∴![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
(2)令![]() ,则
,则![]() ,由题意知方程
,由题意知方程![]() 有两个根
有两个根![]() ,即方程
,即方程![]() 有两个根
有两个根![]() ,不妨设
,不妨设![]() .
.
令![]() ,则
,则![]() ,由
,由![]() 可得
可得![]() ,由
,由![]() 可得
可得![]() ,∴
,∴![]() 时,
时, ![]() 单调递增,
单调递增, ![]() 时,
时, ![]() 单调递减.
单调递减.
根据已知有: ![]() ,要证
,要证![]() ,即证
,即证![]() ,即
,即![]() .
.
即证![]() .令
.令![]() ,下面证
,下面证![]() 对任意的
对任意的![]() 恒成立.
恒成立.
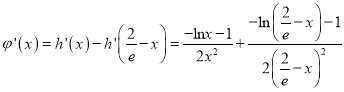 ,∵
,∵![]() ,∴
,∴![]() ,
, ![]() .
.
∴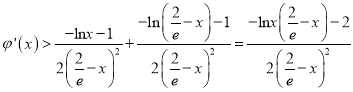 .
.
∵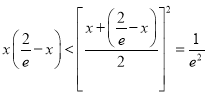 ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() 在
在![]() 是增函数,∴
是增函数,∴![]() ,∴
,∴![]() .
.
点睛: 本题主要考查函数的导数的综合应用,函数的单调性与零点,构造法的应用,考查学生分析问题解决问题的能力,难度比较大.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
【题目】一企业从某条生产线上随机抽取30件产品,测量这些产品的某项技术指标值![]() ,得到如下的频数分布表:
,得到如下的频数分布表:
|
|
|
|
|
频数 | 2 | 6 | 18 | 4 |
(I)估计该技术指标值的平均数;(用各组区间中点值作代表)
(II) 若![]() 或
或![]() ,则该产品不合格,其余的是合格产品,试估计该条生产线生产的产品为合格品的概率;
,则该产品不合格,其余的是合格产品,试估计该条生产线生产的产品为合格品的概率;
(III)生产一件产品,若是合格品可盈利80元,不合格品则亏损10元,在(II)的前提下,从该生产线生产的产品中任取出两件,记![]() 为两件产品的总利润,求随机变量X的分布列和期望.
为两件产品的总利润,求随机变量X的分布列和期望.